机器学习对回归模型的评价指标：均方误差、可解释方差和R方值
学习过概率与统计的同学们都知道，对于线性回归及其他的回归模型来说，评价连续性可拟合的数据就不能使用离散二分类器的评价指标对回归模型进行评价。因此我们引入了均方误差（mean squared error MSE）、可解释方差(Explained Var score)和R方值()。首先我们先看一下这三个概念是如何计算一个评价值(score)的：均方误差：又称MSE，是个使用频度很高的评价指...
学习过概率与统计的同学们都知道，对于线性回归及其他的回归模型来说，评价连续性可拟合的数据就不能使用离散二分类器的评价指标对回归模型进行评价。因此我们引入了均方误差（mean squared error MSE）、可解释方差(Explained Var score)和R方值(
)。
首先我们先看一下这三个概念是如何计算一个评价值(score)的：
均方误差：
又称MSE，是个使用频度很高的评价指标，在概率论和数理统计中的数学定义式就是：
前i个样本属性实际值 
与预测值距离差 
的平方和均值。
MSE衡量的是样本整体与模型预测值偏离程度。
可解释方差：
这部分很少有资料提到可解释方差的公式，根据一些资料的描述，可解释方差是(1- 样本值与预测值之差的方差/样本方差)，数学公式描述为：
E表示均值；
因为是从代码中解读的公式，所以这个公式可能写的有点不太对，望有人指出正确的公式是咋个模样。
看着怪折腾的……
可解释方差指标衡量的是所有预测值和样本之间的差的分散程度与样本本身的分散程度的相近程度。本身是分散程度的对比。最后用1-这个值，最终值越大表示预测和样本值的分散分布程度越相近。
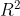值：
又名决定系数，
公式为
这个公式的作为指标的意图就相对明显了。决定系数计算出来越是接近1，预测值越接近真实样本值。
CSDN联合极客时间，共同打造面向开发者的精品内容学习社区，助力成长！
更多推荐
5
0- 0
已为社区贡献1条内容
所有评论(0)