机器学习之感知机(Perceptron)模型
机器学习之Perceptron模型本文主要介绍机器学习领域最为基础的模型,感知机模型:1、感知机模型介绍2、感知机数学原理3、算法及Python代码实现4、小结1、感知机模型介绍定义(感知机)假设输入空间(特征空间)是,输出空间是Y={+1,-1},输入表示实例的特征向量,对应于输入空间(特征空间)的点;输出表示实例的类别。由输入空间到输出空间的如下函数 ...
机器学习之Perceptron模型
本文主要介绍机器学习领域最为基础的模型,感知机模型:
- 1、感知机模型介绍
- 2、感知机数学原理
- 3、算法及Python代码实现
- 4、小结
1、感知机模型介绍
定义(感知机) 假设输入空间(特征空间)是
,输出空间是Y={+1,-1},输入
表示实例的特征向量,对应于输入空间(特征空间)的点;输出
表示实例的类别。由输入空间到输出空间的如下函数 f(x)=sign(w·x+b)称为感知机,其中w和b称为感知机的参数,sign为符号函数定义为
2、感知机数学原理
2.1 感知机学习策略
对于给定一个数据集T={(x1,y1),(x2,y2),…,(xN,yN)},其中,xi∈X=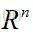
2.2感知机学习策略
首先写出输入空间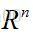
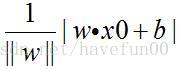
这里||w||是w的L2范数
对于误分类来说,-yi(w·xi+b)>0 成立,因为在误分类情形下yi的值与w·xi+b的值符号相反,又因为yi取值为+1,-1,用yi的值可以去掉上面的距离公式中的绝对值符号,因此误分类点xi到超平面的距离为 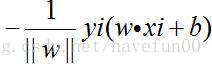
这样,假设超平面S的误分类点集合为M,那么所有误分类点到超平面S的总距离为 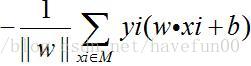
3、算法及Python代码实现
感知机学习算法的原始形式
输入:训练数据TT={(x1,y1),(x2,y2),…,(xN,yN)},其中,xi∈X=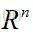
输出:w,b;感知机模型f(x)=sign(w·x+b).
(1)选取初值w0,b0
(2)在训练集中选取数据(xi,yi)
(3)如果yi(w·xi+b)≤0,w ← w+ηyi·xi;b ← b+ηyi
(4)转至(2),直至训练集中没有误分类点
下面始Python实现代码
import numpy as np
import random as random
import matplotlib as mpl
import matplotlib.pyplot as plt
datas = [[(1,2),-1],[(2,1),-1],[(2,2),-1],[(1,4),1],[(3,3),1],[(5,4),1],[(3, 3), 1], [(4, 3), 1], [(1, 1), -1],[(2, 3), -1], [(4, 2), 1]]
random.shuffle(datas)
fig = plt.figure('Input Figure')
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
#plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
xArr = np.array([x[0] for x in datas])
yArr = np.array([x[1] for x in datas])
xPlotx,xPlotx_,xPloty,xPloty_ = [],[],[],[]
for i in range(len(datas)):
y = yArr[i]
if y>0:
xPlotx.append(xArr[i][0])
xPloty.append(xArr[i][1])
else:
xPlotx_.append(xArr[i][0])
xPloty_.append(xArr[i][1])
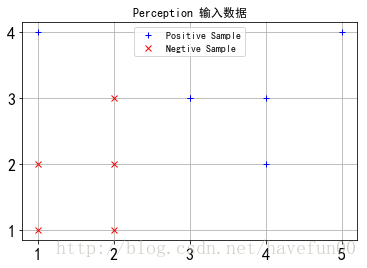
plt.title('Perception 输入数据')
plt.grid(True)
pPlot1,pPlot2 = plt.plot(xPlotx,xPloty,'b+',xPlotx_,xPloty_,'rx')
plt.legend(handles = [pPlot1,pPlot2],labels=['Positive Sample','Negtive Sample'],loc='upper center')
plt.show()输入10个散点图,显示所有离散数据点
w = np.array([1,1])
b = 3
n = 1
while True:
num = 0
for i in range(len(datas)):
num += 1
x = xArr[i]
y = yArr[i]
z = y*(np.dot(w,x)+b)
if z<=0 :
w = w+n*y*x
b = b+n*y
break
if num>=len(datas):
break
fig = plt.figure('Output Figure')
x0 =np.linspace(0,5,100)
w0 = w[0]
w1 = w[1]
x1 = -(w0/w1)*x0-b/w1
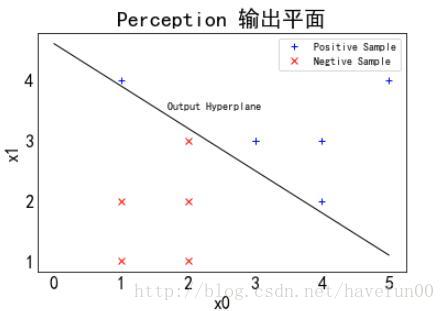
plt.title("Perception 输出平面")
plt.xlabel('x0')
plt.ylabel('x1')
plt.annotate('Output Hyperplane',xy=(0.5,4.5),xytext=(1.7,3.5))
plt.plot(x0,x1,'k', lw=1)
pPlot3, pPlot4= plt.plot(xPlotx,xPloty,'b+',xPlotx_,xPloty_,'rx')
plt.legend(handles = [pPlot3,pPlot4],labels=['Positive Sample','Negative Sample'],loc='upper right')
plt.show()输出得到的超平面S的方程w·x+b=0函数式
4、小结
本次博客主要介绍了感知机模型的原始形式,另外感知机模型还有对偶形式的表达式,这里不再介绍,感知机模型虽然简单,却有很重要的作用,后面我们会讲到SVM支持向量机,理解了感知机模型原理后对后面理解SVM会有很大的帮助。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容
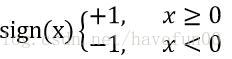
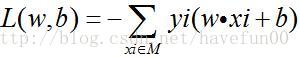








所有评论(0)