林轩田机器学习技法关于特征学习系列，其中涉及到 Neural Network <script type="math/tex" id="MathJax-Element-1">Neural\ Network</script>， Backpropagation Algorithm <script type="math/tex" id="MathJax-Element-2">Backpropagation\ Algorithm</script>， Deep Learning <script type="math/tex" id="MathJax-Element-3">Deep\ Learning</script>， Autoencoder <script type="math/tex" id="MathJax-Element-4">Autoencoder</script>，
PCA <script type="math/tex" id="MathJax-Element-5">PCA</script>， Radial Basis Function Network <script type="math/tex" id="MathJax-Element-6">Radial\ Basis\ Function\ Network</script>， K <script type="math/tex" id="MathJax-Element-7">K</script>-Means<script type="math/tex" id="MathJax-Element-8">Means</script>， Matrix Factorization <script type="math/tex" id="MathJax-Element-9">Matrix\ Factorization</script> 等。

• 机器学习笔记-Neural Network
• 机器学习笔记-Deep Learning
• 机器学习笔记-Radial Basis Function Network
• 机器学习笔记-Matrix Factorization

Radial Basis Function Network

先从一个之前介绍过的模型 Gassian SVM <script type="math/tex" id="MathJax-Element-310">Gassian\ SVM</script> 说起，简单的来说这个模型就是在 SVM <script type="math/tex" id="MathJax-Element-311">SVM</script>中加入了高斯核函数，从而可以做到在无限维度的空间中找最大分隔超平面。该模型最终得到的分类器如下：

<script type="math/tex; mode=display" id="MathJax-Element-312">g_{svm}(x) = sign\bigg(\sum_{SV}\alpha_ny_nexp\big(-\gamma\|x-x_n\|^2\big) + b\bigg)\tag1</script>

仅仅从最终得到的结果来看， Gassian SVM <script type="math/tex" id="MathJax-Element-313">Gassian\ SVM</script>可以看做是一些高斯函数的线性组合，这些高斯函数的中心点是 support vector <script type="math/tex" id="MathJax-Element-314">support\ vector</script>，这些线性组合的系数是 αnyn <script type="math/tex" id="MathJax-Element-315">\alpha_ny_n</script>。

Radial basis function <script type="math/tex" id="MathJax-Element-316">Radial\ basis\ function</script>指的是我们要计算的函数的结果只和距离 (∥x−xn∥) <script type="math/tex" id="MathJax-Element-317">(\|x-x_n\|)</script>有关；

Radial basis function <script type="math/tex" id="MathJax-Element-318">Radial\ basis\ function</script>：径向基函数是一个取值仅仅依赖于离原点距离的实值函数。也就是 Φ(x)=Φ(∥x∥) <script type="math/tex" id="MathJax-Element-319">\Phi(x)=\Phi(\|x\|)</script>，或者还可以是到任意一点 c <script type="math/tex" id="MathJax-Element-320">c</script>的距离，c<script type="math/tex" id="MathJax-Element-321">c</script>点称为中心点，也就是 Φ(x,c)=Φ(∥x−c∥) <script type="math/tex" id="MathJax-Element-322">\Phi(x, c)=\Phi(\|x-c\|)</script> 。

我们记 gn(x)=ynexp(−γ∥x−xn∥2) <script type="math/tex" id="MathJax-Element-323">g_n(x) = y_nexp(-\gamma\|x-x_n\|^2)</script>，这个式子可以理解为，看看 x <script type="math/tex" id="MathJax-Element-324">x</script>和中心点xn<script type="math/tex" id="MathJax-Element-325">x_n</script>的距离，离得越近， exp(−γ∥x−xn∥2) <script type="math/tex" id="MathJax-Element-326">exp(-\gamma\|x-x_n\|^2)</script>的值越大，那么就给出越大的和样本 (xn,yn) <script type="math/tex" id="MathJax-Element-327">(x_n, y_n)</script>同方向上（同号）的得分 ynexp(−γ∥x−xn∥2) <script type="math/tex" id="MathJax-Element-328">y_nexp(-\gamma\|x-x_n\|^2)</script>。最终 (1) <script type="math/tex" id="MathJax-Element-329">(1)</script>式就可以理解为一个新的 x <script type="math/tex" id="MathJax-Element-330">x</script>到不同的中心xn<script type="math/tex" id="MathJax-Element-331">x_n</script>的得分 gn(x) <script type="math/tex" id="MathJax-Element-332">g_n(x)</script>在参数 αn <script type="math/tex" id="MathJax-Element-333">\alpha_n</script>下的线性组合 gsvm(x)=sign(∑svαngn(xn)+b) <script type="math/tex" id="MathJax-Element-334">g_{svm}(x) = sign(\sum_{sv}\alpha_ng_n(x_n) + b)</script>。

这样的话这个模型就可以理解为是一些和支撑向量 (support vector) <script type="math/tex" id="MathJax-Element-335">(support\ vector)</script>有关的径向基函数 (radial basis function) <script type="math/tex" id="MathJax-Element-336">(radial\ basis\ function)</script>的线性组合 (linear aggregation) <script type="math/tex" id="MathJax-Element-337">(linear\ aggregation)</script>。
这一篇要介绍的 Radial basis function network(RBFNetwork) <script type="math/tex" id="MathJax-Element-338">Radial\ basis\ function\ network(RBFNetwork)</script>就是这样的模型的延伸：组合只与半径 (∥x−xn∥) <script type="math/tex" id="MathJax-Element-339">(\|x-x_n\|)</script>有关的函数，从而得到好的学习结果。

如果把 RBFNetwork <script type="math/tex" id="MathJax-Element-340">RBFNetwork</script>的架构画出来和 neural network <script type="math/tex" id="MathJax-Element-341">neural\ network</script>是非常相似的，这可能也是其称为 network <script type="math/tex" id="MathJax-Element-342">network</script>的原因。如下图：

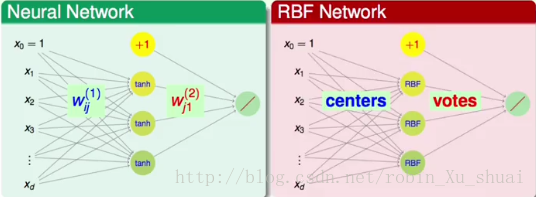
可以看到在 RBFNetwork <script type="math/tex" id="MathJax-Element-343">RBFNetwork</script>的中间一层，借用 neural network <script type="math/tex" id="MathJax-Element-344">neural\ network</script>的概念，也就是隐层中，共有 m <script type="math/tex" id="MathJax-Element-345">m</script>个节点，分别表示m<script type="math/tex" id="MathJax-Element-346">m</script>个中心点，这一层的功能就是计算样本点到每一个中心点的 RBF <script type="math/tex" id="MathJax-Element-347">RBF</script>函数值，然后再在输出层进行 linear aggregation <script type="math/tex" id="MathJax-Element-348">linear\ aggregation</script>。 RBFNetwork <script type="math/tex" id="MathJax-Element-349">RBFNetwork</script>是 neural network <script type="math/tex" id="MathJax-Element-350">neural\ network</script>的一个分支，它研究的是将 neural network <script type="math/tex" id="MathJax-Element-351">neural\ network</script>中的神经元的功能从计算权重和输入的內积变为计算一个有关距离的函数值时，模型可以取得怎么样的效果。

RBF Network Hypothesis

现在我们可以使用下面的式子来描述不同的 RBFNetwork <script type="math/tex" id="MathJax-Element-52">RBFNetwork</script>的形式：

<script type="math/tex; mode=display" id="MathJax-Element-53">h(x) = Output\bigg(\sum_{m = 1}^{M}\beta_mRBF(x, \mu_m) + b\bigg)</script>

其中： RBF(x,μm) <script type="math/tex" id="MathJax-Element-54">RBF(x, \mu_m)</script>可以是高斯或者是其他的距离的函数， μn <script type="math/tex" id="MathJax-Element-55">\mu_n</script>是中心点向量， βm <script type="math/tex" id="MathJax-Element-56">\beta_m</script>是线性组合的系数， Output <script type="math/tex" id="MathJax-Element-57">Output</script>的方式视要解决的问题是回归还是分类而定。这里面有两个比较关键的因素， 一个需要参考的中心点 μm <script type="math/tex" id="MathJax-Element-58">\mu_m</script>有哪些，另一个是线性组合的系数 βm <script type="math/tex" id="MathJax-Element-59">\beta_m</script>怎么来决定。例如对于 Gaussian SVM <script type="math/tex" id="MathJax-Element-60">Gaussian\ SVM</script>来说： RBF <script type="math/tex" id="MathJax-Element-61">RBF</script>是高斯函数；由于要解决的是二元分类问题，所以 Output <script type="math/tex" id="MathJax-Element-62">Output</script>采用的函数是 sign <script type="math/tex" id="MathJax-Element-63">sign</script>； M <script type="math/tex" id="MathJax-Element-64">M</script>的大小是支持向量的个数；μm<script type="math/tex" id="MathJax-Element-65">\mu_m</script>是支持向量； βm <script type="math/tex" id="MathJax-Element-66">\beta_m</script>是对偶 SVM <script type="math/tex" id="MathJax-Element-67">SVM</script>问题的解 αm <script type="math/tex" id="MathJax-Element-68">\alpha_m</script>和支持向量的 label <script type="math/tex" id="MathJax-Element-69">label</script>值 ym <script type="math/tex" id="MathJax-Element-70">y_m</script>的乘积。

所以一般的来说， RBFNetwork <script type="math/tex" id="MathJax-Element-71">RBFNetwork</script>需要决定的就是中心点 μm <script type="math/tex" id="MathJax-Element-72">\mu_m</script>和线性组合的系数 βm <script type="math/tex" id="MathJax-Element-73">\beta_m</script>，另外还有一个参数，例如 RBF <script type="math/tex" id="MathJax-Element-74">RBF</script>函数的选择以及 Output <script type="math/tex" id="MathJax-Element-75">Output</script>的输出方式。

在SVM with Gaussian Kernel中曾经提到， Kernel function <script type="math/tex" id="MathJax-Element-76">Kernel\ function</script>的结果简单来说就是两个向量转换到高维空间中的內积，既然是內积因此可以理解为是一种衡量相似性的方法，即原来两个低维空间向量的相似性通过转换到高维空间计算內积来描述。 Poly <script type="math/tex" id="MathJax-Element-77">Poly</script>核中隐藏着一个多项式转换，也可以说其描述的是一个更高维空间中的相似性，同理高斯函数中隐藏着一个无限维空间中的相似性。
而在这里的 RBF <script type="math/tex" id="MathJax-Element-78">RBF</script>也是一种相似性的衡量，不过是直接通过在 X <script type="math/tex" id="MathJax-Element-79">X</script>空间中的距离来计算的，例如高斯函数，就是将距离的平方取负号然后exp<script type="math/tex" id="MathJax-Element-80">exp</script>就可以描述相似性。所以只要距离能算出来就可以定义不同的 RBF <script type="math/tex" id="MathJax-Element-81">RBF</script>。
所以 Kernel <script type="math/tex" id="MathJax-Element-82">Kernel</script>和 RBF <script type="math/tex" id="MathJax-Element-83">RBF</script>可以看成是两种相似性的衡量方法，而 Gaussian <script type="math/tex" id="MathJax-Element-84">Gaussian</script>是这两种方式的交集。

RBFNetwork <script type="math/tex" id="MathJax-Element-85">RBFNetwork</script>告诉我们一个很重要的事情是：相似性是一种很好的定义特征转换的方法，所以当有另外的相似性的衡量方法，和 kernel <script type="math/tex" id="MathJax-Element-86">kernel</script>无关，和 RBF <script type="math/tex" id="MathJax-Element-87">RBF</script>无关，那么就可以利用这些相似性作为特征转化来提高学习的效果。

如下的三个函数都可以看做是 RBF <script type="math/tex" id="MathJax-Element-88">RBF</script>：

• exp(−γ∥x−μ∥2) <script type="math/tex" id="MathJax-Element-89">exp(-\gamma\|x-\mu\|^2)</script>
• −xTx−2xTμ+μTμ−−−−−−−−−−−−−−−√ <script type="math/tex" id="MathJax-Element-90">-\sqrt{x^Tx - 2x^T\mu + \mu^T\mu}</script>
• ∥x=μ∥ <script type="math/tex" id="MathJax-Element-91">\|x = \mu\|</script>

RBF Network Learning

上一小节介绍了 RBF <script type="math/tex" id="MathJax-Element-92">RBF</script>的基本概念

h(x)=Output(∑m=1MβmRBF(x,μm))

<script type="math/tex; mode=display" id="MathJax-Element-93">h(x) = Output\bigg(\sum_{m = 1}^{M}\beta_mRBF(x, \mu_m)\bigg)</script>

其中一个需要解决的问题是中心点 μm <script type="math/tex" id="MathJax-Element-94">\mu_m</script>如何选取，一个简单的解决方法是将每一个数据都当做是中心点，这样的 RBFNetwork <script type="math/tex" id="MathJax-Element-95">RBFNetwork</script>称为 Full RBFNetwork <script type="math/tex" id="MathJax-Element-96">Full\ RBFNetwork</script>。

Full RBFNetwork：M=N <script type="math/tex" id="MathJax-Element-97">Full\ RBFNetwork： M = N</script>(资料量)， μm=xm <script type="math/tex" id="MathJax-Element-98">\mu_m =x_m</script>。这样的方式可以理解为每一个已知的数据都会参与对未知数据的预测，只不过对预测结果的贡献取决于和未知样本的相似性或者说距离。例如，对于二分类问题来说， ym∈{−1,+1} <script type="math/tex" id="MathJax-Element-99">y_m \in \{-1, +1\}</script>， full RBF network <script type="math/tex" id="MathJax-Element-100">full\ RBF\ network</script>构成的分类器如下：

guniform(x)=sign(∑m=1Nymexp(−γ∥x−xm∥2))(2)

<script type="math/tex; mode=display" id="MathJax-Element-101">g_{uniform}(x) = sign\bigg(\sum_{m = 1}^{N}y_mexp(-\gamma\|x-x_m\|^2)\bigg)\tag2</script>

Nearest Neighbors

由于不知道该如何选取中心点而把所有的样本都视为中心，其实对这样的方式稍加改进就能得到另一种十分常见的机器学习方法： K <script type="math/tex" id="MathJax-Element-102">K</script>-NN<script type="math/tex" id="MathJax-Element-103">NN</script>，即 k <script type="math/tex" id="MathJax-Element-104">k</script>近邻。

在2<script type="math/tex" id="MathJax-Element-105">2</script>式所示的 uniform full RBF network <script type="math/tex" id="MathJax-Element-106">uniform\ full\ RBF\ network</script>中，可以理解为是在计算 N <script type="math/tex" id="MathJax-Element-107">N</script>个高斯函数的结果的线性组合，这些高斯函数的值有大有小，其中和x<script type="math/tex" id="MathJax-Element-108">x</script>最相近的 xm <script type="math/tex" id="MathJax-Element-109">x_m</script>所在的那个高斯函数取得最大的值，由于高斯函数衰减的很快，所以通常值最大的高斯函数给出的结果往往能够决定最终的结果，这样我们就可以使用高斯函数值最大的那个中心点的 label <script type="math/tex" id="MathJax-Element-110">label</script>作为对结果的预测，而不用对所有的高斯函数的结果进行求和。（这个时候模型由 aggregation <script type="math/tex" id="MathJax-Element-111">aggregation</script>变为 selection <script type="math/tex" id="MathJax-Element-112">selection</script>）。其实就是在所有的样本中找一个和待预测样本最相似的样本将其 label <script type="math/tex" id="MathJax-Element-113">label</script>做为待预测的样本的 label <script type="math/tex" id="MathJax-Element-114">label</script>。将这样的方式进行延伸就得到了 k nearest neighbors <script type="math/tex" id="MathJax-Element-115">k\ nearest\ neighbors</script>，即找和待预测样本最相似的 k <script type="math/tex" id="MathJax-Element-116">k</script> 个样本，对这些样本点的label<script type="math/tex" id="MathJax-Element-117">label</script>做 voting <script type="math/tex" id="MathJax-Element-118">voting</script>。

不管是 uniform full RBF network <script type="math/tex" id="MathJax-Element-119">uniform\ full\ RBF\ network</script> 还是 k nearest neighbors <script type="math/tex" id="MathJax-Element-120">k\ nearest\ neighbors</script>，可以看到在训练阶段只是做了数据的存储，所有的工作量都集中到了预测阶段。

Interpolation by full RBF network

上面介绍了 full RBF network <script type="math/tex" id="MathJax-Element-121">full\ RBF\ network</script>，但是其中用来组合高斯函数的参数被简单的设置为了 ym <script type="math/tex" id="MathJax-Element-122">y_m</script>，这里我们对其进行改进，学习得到最佳的参数 βm <script type="math/tex" id="MathJax-Element-123">\beta_m</script>。并且我们的目标是使用 full RBF network <script type="math/tex" id="MathJax-Element-124">full\ RBF\ network</script>来做 regression <script type="math/tex" id="MathJax-Element-125">regression</script>。即我们希望得到的模型是：

h(x)=(∑m=1NβmRBF(x,xm))

<script type="math/tex; mode=display" id="MathJax-Element-126">h(x) = \bigg(\sum_{m=1}^{N}\beta_mRBF(x, x_m)\bigg)</script>

要求得最佳的 βm <script type="math/tex" id="MathJax-Element-127">\beta_m</script>，其实就是要在通过 RBF <script type="math/tex" id="MathJax-Element-128">RBF</script>进行转换之后的数据： zn={RBF(xn,x1),RBF(xn,x2),⋯,RBF(xn,xN)},n=1,2,⋯.N <script type="math/tex" id="MathJax-Element-129">z_n = \{RBF(x_n, x_1), RBF(x_n, x_2),\cdots, RBF(x_n, x_N)\}, n = 1, 2, \cdots. N</script>上做一个线性回归。可以得到线性回归的最佳解：

β=(ZTZ)−1ZTy

<script type="math/tex; mode=display" id="MathJax-Element-130">\beta = (Z^TZ)^{-1}Z^Ty</script>
其中

• • Z <script type="math/tex" id="MathJax-Element-131">Z</script>是一个N×N<script type="math/tex" id="MathJax-Element-132">N\times N</script>的对称矩阵 (zi.j=RBF(xi,xj)=RBF(xj,xi)=zj,i) <script type="math/tex" id="MathJax-Element-133">(z_{i.j} = RBF(x_i, x_j) = RBF(x_j, x_i) = z_{j, i})</script>。
  • 当所有的 xn <script type="math/tex" id="MathJax-Element-134">x_n</script>不同的时候，使用高斯函数计算得到的 Z <script type="math/tex" id="MathJax-Element-135">Z</script>矩阵是可逆的。

  因为Z<script type="math/tex" id="MathJax-Element-136">Z</script>是对称的， 是可逆的，所以有 β=(ZTZ)−1ZTy=Z−1Z−1Zy=Z−1y <script type="math/tex" id="MathJax-Element-137">\beta = (Z^TZ)^{-1}Z^Ty = Z^{-1}Z^{-1}Zy = Z^{-1}y</script>

  所以当使用 Gaussian <script type="math/tex" id="MathJax-Element-138">Gaussian</script>函数作为 RBF <script type="math/tex" id="MathJax-Element-139">RBF</script>，每一个数据点都作为中心点，并且资料不重复的话，那么最佳的 βm <script type="math/tex" id="MathJax-Element-140">\beta_m</script>有很简单的解析解 β=Z−1y <script type="math/tex" id="MathJax-Element-141">\beta = Z^{-1}y</script>。

  这样我们就得到了 full Gaussian RBF network for regression <script type="math/tex" id="MathJax-Element-142">full\ Gaussian\ RBF\ network\ for\ regression</script>的模型，如下：
  

  gRBF=(∑m=1NZ−1y exp∥x−xm∥2)
  <script type="math/tex; mode=display" id="MathJax-Element-143">g_{RBF} = \bigg(\sum_{m=1}^{N}Z^{-1}y\ exp\|x-x_m\|^2\bigg)</script>

  我们来分析看看这样的模型有什么特别之处。当我们把训练集中的一个样本的 xn <script type="math/tex" id="MathJax-Element-144">x_n</script> 喂给该模型的时候发现经过该模型计算之后会得到该样本的 yn <script type="math/tex" id="MathJax-Element-145">y_n</script> 值。具体的计算过程如：
  

  gRBF(x1)=βTz1=(Z−1y)T(first column of Z)=yTZ−1(first column of Z)=yT[1 0 ⋯ 0]T=y1
  <script type="math/tex; mode=display" id="MathJax-Element-146">g_{RBF}(x_1) = \beta^Tz_1 = (Z^{-1}y)^T(first\ column\ of\ Z) = y^TZ^{-1}(first\ column\ of\ Z) = y^T[1\ 0\ \cdots\ 0]^T = y_1</script>
  其中， ZT=Z⟶(Z−1)T=Z−1，ZTZ=I <script type="math/tex" id="MathJax-Element-147">Z^T = Z\longrightarrow (Z^{-1})^T = Z^{-1}， Z^TZ = I</script>

  也就是说 gRBF <script type="math/tex" id="MathJax-Element-148">g_{RBF}</script>在训练集上的错误率为 0 <script type="math/tex" id="MathJax-Element-149">0</script>。这样的结果对于一些应用例如函数逼近function approximation<script type="math/tex" id="MathJax-Element-150">function\ approximation</script>来说是完美的，因为经过拟合的函数通过了每一个已知的样本点，但是对于 machine learning <script type="math/tex" id="MathJax-Element-151">machine\ learning</script>来说不是一个好的结果，因为这可能有 overfitting <script type="math/tex" id="MathJax-Element-152">overfitting</script>的风险。

  Regularized full RBF network

  在线性回归 linear regression <script type="math/tex" id="MathJax-Element-153">linear\ regression</script>中，通过加入正则化项来防止过拟合，加了正则化项的 linear regression <script type="math/tex" id="MathJax-Element-154">linear\ regression</script>称为 ridge regression <script type="math/tex" id="MathJax-Element-155">ridge\ regression</script>。此时求得的 regularized full RBFNet for regression <script type="math/tex" id="MathJax-Element-156">regularized\ full\ RBFNet\ for\ regression</script>的最佳的 β <script type="math/tex" id="MathJax-Element-157">\beta</script>为：
  

  β=(ZTZ+λI)−1ZTy(3)
  <script type="math/tex; mode=display" id="MathJax-Element-158">\beta = (Z^TZ+\lambda I)^{-1}Z^Ty\tag3</script>

  在 kernel ridge regressrion <script type="math/tex" id="MathJax-Element-159">kernel\ ridge\ regressrion</script> 中最佳的 β <script type="math/tex" id="MathJax-Element-160">\beta</script>为：

  β=(K+λI)−1y(4)
  <script type="math/tex; mode=display" id="MathJax-Element-161">\beta = (K+\lambda I)^{-1}y\tag4</script>

  可以看到 (3) <script type="math/tex" id="MathJax-Element-162">(3)</script>和 (4) <script type="math/tex" id="MathJax-Element-163">(4)</script>式非常的相近，因为 RBFNet <script type="math/tex" id="MathJax-Element-164">RBFNet</script>中的 Z <script type="math/tex" id="MathJax-Element-165">Z</script>其实就等于高斯核矩阵K<script type="math/tex" id="MathJax-Element-166">K</script>，而产生差别的原因在于 regularization <script type="math/tex" id="MathJax-Element-167">regularization</script>的方式不同，在 kernel ridge regressrion <script type="math/tex" id="MathJax-Element-168">kernel\ ridge\ regressrion</script>中是针对无限多维的转换做 regularization <script type="math/tex" id="MathJax-Element-169">regularization</script>，在 regularized full RBFNet <script type="math/tex" id="MathJax-Element-170">regularized\ full\ RBFNet</script>中是对有限维度的转换做 regularization <script type="math/tex" id="MathJax-Element-171">regularization</script>。

  以上的讨论都是基于所有的资料都用作中心点的情况，我们说这样可能会出现 overfitting <script type="math/tex" id="MathJax-Element-172">overfitting</script>，所以需要添加 regularizer <script type="math/tex" id="MathJax-Element-173">regularizer</script>。借鉴 SVM <script type="math/tex" id="MathJax-Element-174">SVM</script>中 support vector <script type="math/tex" id="MathJax-Element-175">support\ vector</script>的结果，当不使用所有的数据点都作为中心点的时候，可能会有更好的结果。用比较少的中心点也可以当成是在做 regularization <script type="math/tex" id="MathJax-Element-176">regularization</script>， 因为这样的话第二层的权重就变少了。下一节我们将介绍如何从所有的数据点中选择出具有代表性的数据点作为中心点。

  k-Means Algorithm

  这一小节我们的主要目标是找一些有代表性的样本作为 RBFNetwork <script type="math/tex" id="MathJax-Element-177">RBFNetwork</script>的中心点，而不是将所有的样本都当成是 RBFNetwork <script type="math/tex" id="MathJax-Element-178">RBFNetwork</script>的中心点。因为当 x1≈x2 <script type="math/tex" id="MathJax-Element-179">x_1 \approx x_2</script>的时候，它们的径向基函数表达的意思也是差不多的，这样就可以找一些比较有代表性的样本点来构成最终的 RBF Network <script type="math/tex" id="MathJax-Element-180">RBF\ Network</script>，而不必在做预测的时候考虑所有点的影响。接下来可以看到， 在解决这个问题的过程中，我们推导出了聚类算法 k <script type="math/tex" id="MathJax-Element-181">k</script>-Means<script type="math/tex" id="MathJax-Element-182">Means</script>，并从数学的角度或者说是最优化的角度重新认识了这个简单但是十分有用的算法。

  这个找有代表性的样本点的问题可以转化为聚类问题，因为当对数据聚类完成之后，每一个类的聚类中心就是我们想要找的 RBF Network <script type="math/tex" id="MathJax-Element-183">RBF\ Network</script>中具有代表性的点。

  对于聚类问题，我们希望每一个类中的样本点要尽可能的相似，即， 如果 x1,x2∈Sm <script type="math/tex" id="MathJax-Element-184">x_1, x_2 \in S_m</script>，那么 μm≈x1≈x2 <script type="math/tex" id="MathJax-Element-185">\mu_m \approx x_1 \approx x_2</script>。（假设 μm <script type="math/tex" id="MathJax-Element-186">\mu_m</script>是 Sm <script type="math/tex" id="MathJax-Element-187">S_m</script>的聚类中心，也就是我们想要找的代表点）同样我们也可以定义一个损失函数如下：
  

  Ein(S1,⋯,SM;μ1,⋯,μM)=1N∑n=1N∑m=1M[[xn∈Sm]]∥xn−μm∥2(1)
  <script type="math/tex; mode=display" id="MathJax-Element-188">E_{in}(S_1, \cdots, S_M;\mu_1, \cdots,\mu_M) = \frac1N\sum_{n=1}^{N}\sum_{m=1}^{M}[[x_n \in S_m]]\|x_n - \mu_m\|^2\tag1</script>
  我们想要 Ein <script type="math/tex" id="MathJax-Element-189">E_{in}</script>最小， 其中：如果 ◯ <script type="math/tex" id="MathJax-Element-190">\bigcirc</script>成立， [[◯]]=1 <script type="math/tex" id="MathJax-Element-191">[[\bigcirc]] = 1</script>；如果 ◯ <script type="math/tex" id="MathJax-Element-192">\bigcirc</script>不成立， [[◯]]=0 <script type="math/tex" id="MathJax-Element-193">[[\bigcirc]] = 0</script>， N <script type="math/tex" id="MathJax-Element-194">N</script>为样本的个数， M<script type="math/tex" id="MathJax-Element-195">M</script>为聚类的个数。直观上讲，1式就是要最小化所有样本点到聚类中心点的距离。一方面我们要找到最佳的数据聚类方式，这是一个组合最优化问题；另一方面我们需要找到最佳的中心点选取方式，这是一个数值最优化问题。也就是需要决定两组参数 {S1,⋯,Sm},{μ1,⋯,μM} <script type="math/tex" id="MathJax-Element-196">\{S_1, \cdots, S_m\}, \{\mu_1, \cdots, \mu_M\}</script>，在这里我们采取的优化方式是进行交替的优化， optimize alternatingly <script type="math/tex" id="MathJax-Element-197">optimize\ alternatingly</script>。

  当 μ1,⋯,μM <script type="math/tex" id="MathJax-Element-198">\mu_1, \cdots, \mu_M</script>固定的时候，也就是聚类中心已经固定下来了， 现在只需要考虑对于一个样本点 xn <script type="math/tex" id="MathJax-Element-199">x_n</script>来说，如何决定其归属的类，根据1式很容易得到，当选择使得 ∥xn−μm∥ <script type="math/tex" id="MathJax-Element-200">\|x_n - \mu_m\|</script>最小的 Sm <script type="math/tex" id="MathJax-Element-201">S_m</script>，也就是离 xn <script type="math/tex" id="MathJax-Element-202">x_n</script>最近的聚类中心所在的类作为 xn <script type="math/tex" id="MathJax-Element-203">x_n</script>所属的类别时 Ein <script type="math/tex" id="MathJax-Element-204">E_{in}</script>最小。
  问题解决了一半， 当每一个样本点都决定了其归属的类别之后，接下来就可以更新每一个类的中心.

  通常我们会将类中数据点的均值作为该类新的聚类中心， 为什么这么做呢？

  当 S1,⋯,Sm <script type="math/tex" id="MathJax-Element-205">S_1, \cdots, S_m</script>固定的时候，最小化 Ein <script type="math/tex" id="MathJax-Element-206">E_{in}</script>的问题就变成了针对变量 μ <script type="math/tex" id="MathJax-Element-207">\mu</script>的一个无约束的最优化问题。当然毫不犹豫的求取梯度：

  ▽μmEin=∂(∑Nn=1∑Mm=1[[xn∈Sm]]∥xn−μm∥2)∂μm=−2∑n=1N[[xn∈Sm]](xn−μm)=−2(∑xn∈Smxn−|Sm|μm)
  <script type="math/tex; mode=display" id="MathJax-Element-208">\begin{align*} \bigtriangledown_{\mu_m}E_{in} &= \frac{\partial\bigg( \sum_{n=1}^{N}\sum_{m=1}^{M}[[x_n \in S_m]]\|x_n - \mu_m\|^2\bigg)}{\partial\mu_m} \\ &= -2\sum_{n=1}^{N}[[x_n \in S_m]](x_n - \mu_m) \\ &= -2\bigg(\sum_{x_n \in S_m}x_n - |S_m|\mu_m\bigg) \end{align*}</script>

  令梯度为 0 <script type="math/tex" id="MathJax-Element-209">0</script>求取最佳解。
  

  −2(∑xn∈Smxn−|Sm|μm)=0⟶μm=∑xn∈Smxn|Sm|
  <script type="math/tex; mode=display" id="MathJax-Element-210">-2\bigg(\sum_{x_n \in S_m}x_n - |S_m|\mu_m\bigg) = 0\longrightarrow\mu_m = \frac{\sum_{x_n \in S_m}x_n}{ |S_m|}</script>

  这样我们就得到了一个非常著名的无监督学习算法， k <script type="math/tex" id="MathJax-Element-211">k</script>-Means<script type="math/tex" id="MathJax-Element-212">Means</script>聚类算法。上面的谈论给了一些不同的视角来看待这个算法的运作。

  k Means Algorithm <script type="math/tex" id="MathJax-Element-213">k\ Means\ Algorithm</script>

  • 随机从数据中选择 k <script type="math/tex" id="MathJax-Element-214">k</script> 个数据点作为初始的聚类中心
  • repeate<script type="math/tex" id="MathJax-Element-215">repeate</script>
    
    • 将每一个样本点归属到离它最近的聚类中心，从而得到k个类
    • 求取每一个类中的均值作为新的聚类中心
  • until converge <script type="math/tex" id="MathJax-Element-216">until\ converge</script>

  为什么该算法一定会收敛呢？也就是说为什么经过一定次数的迭代之后{S_1, \cdots, S_m}会不在发生变化而稳定呢？经过上面的分析我们知道，每一个步骤，不过是确定了中心划分数据点， 还是确定了类簇决定新的聚类中心，都是在最小化 Ein <script type="math/tex" id="MathJax-Element-217">E_{in}</script>，而 Ein <script type="math/tex" id="MathJax-Element-218">E_{in}</script>的下限为 0 <script type="math/tex" id="MathJax-Element-219">0</script>， 所以该算法一定会收敛。

  RBF Network Using k-Means

  我们之所以会推导k<script type="math/tex" id="MathJax-Element-220">k</script>- Means <script type="math/tex" id="MathJax-Element-221">Means</script>这个算法，是为了确定 RBF Network <script type="math/tex" id="MathJax-Element-222">RBF\ Network</script>的中心点。结合 k <script type="math/tex" id="MathJax-Element-223">k</script>-Means<script type="math/tex" id="MathJax-Element-224">Means</script>得到的 RBFNetwork <script type="math/tex" id="MathJax-Element-225">RBFNetwork</script>算法如下：

  RBF Network Using kMeans <script type="math/tex" id="MathJax-Element-226">RBF\ Network\ Using\ k Means</script>

  • run kMeans with k=M to get {μm} <script type="math/tex" id="MathJax-Element-227">run\ kMeans\ with\ k=M\ to\ get\ \{\mu_m\}</script>
  • construct transform Φ(x) from RBF at μm:Φ(x)=[RBF(x,μ1),RBF(x,μ2),⋯,RBF(x,μM)] <script type="math/tex" id="MathJax-Element-228">construct\ transform\ \Phi(x)\ from\ RBF\ at\ \mu_m:\Phi(x) = [RBF(x, \mu_1), RBF(x, \mu_2), \cdots, RBF(x, \mu_M)]</script>
  • run linear model on {(ϕ(xn),yn)} get β <script type="math/tex" id="MathJax-Element-229">run\ linear\ model\ on\ \{(\phi(x_n), y_n)\}\ get\ \beta</script>
  • return grbfNet(x)=LinearHypothesis(β,Φ(x)) <script type="math/tex" id="MathJax-Element-230">return\ g_{rbfNet}(x) = LinearHypothesis(\beta, \Phi(x))</script>

  首先使用 k <script type="math/tex" id="MathJax-Element-231">k</script>-Means<script type="math/tex" id="MathJax-Element-232">Means</script>算法来得到样本的 M <script type="math/tex" id="MathJax-Element-233">M</script>个中心点，我们利用这些中心点结合径向基函数RBF<script type="math/tex" id="MathJax-Element-234">RBF</script>定义特征转换 Φ(x) <script type="math/tex" id="MathJax-Element-235">\Phi(x)</script>，原始数据经过特征转换得到新的数据 Φ(x)=[RBF(x,μ1),RBF(x,μ2),⋯,RBF(x,μM)] <script type="math/tex" id="MathJax-Element-236">\Phi(x) = [RBF(x, \mu_1), RBF(x, \mu_2), \cdots, RBF(x, \mu_M)]</script>， 在这些数据上利用线性模型： linear regression,logistic regression,linear SVM <script type="math/tex" id="MathJax-Element-237">linear\ regression, logistic\ regression, linear\ SVM</script>等等来求解 β <script type="math/tex" id="MathJax-Element-238">\beta</script>，得到最后的 RBF Network <script type="math/tex" id="MathJax-Element-239">RBF\ Network</script>。

  这是我们第二次看到使用非监督的学习算法来萃取数据中的特征，第一次是利用 autoencoder <script type="math/tex" id="MathJax-Element-240">autoencoder</script>。

  在 RBF Network <script type="math/tex" id="MathJax-Element-241">RBF\ Network</script>中的参数主要有 M <script type="math/tex" id="MathJax-Element-242">M</script>：中心点的个数；RBF<script type="math/tex" id="MathJax-Element-243">RBF</script>中的参数，例如如果使用 Gaussian <script type="math/tex" id="MathJax-Element-244">Gaussian</script>的话需要决定其中的 λ <script type="math/tex" id="MathJax-Element-245">\lambda</script>。

  k-Means and RBF Network in Action

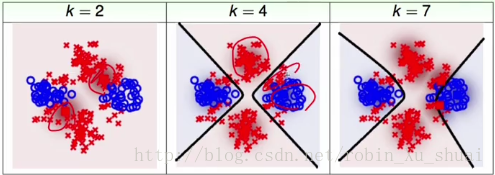
  k <script type="math/tex" id="MathJax-Element-365">k</script>-Means<script type="math/tex" id="MathJax-Element-366">Means</script>算法的结果受给定的参数 k <script type="math/tex" id="MathJax-Element-367">k</script> 和初始聚类中心设定的影响，因为在求解的过程中使用的方法是alternating optimization<script type="math/tex" id="MathJax-Element-368">alternating\ optimization</script>所以并不一定会保证得到全局最优的解。

  下面的图给出了一个利用 RBFNetwork Using kMeans <script type="math/tex" id="MathJax-Element-369">RBFNetwork\ Using\ kMeans</script>做二分类的例子，

  
  

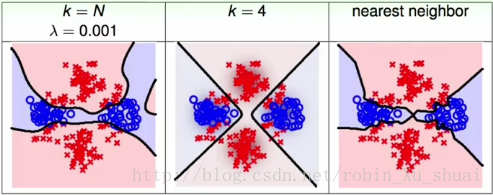
  从上图可以得到的结论是， 当使用 k <script type="math/tex" id="MathJax-Element-370">k</script>-Means<script type="math/tex" id="MathJax-Element-371">Means</script>方法能够找出更合理的数据中心点或者说数据的代表的时候，那么 RBF Network <script type="math/tex" id="MathJax-Element-372">RBF\ Network</script>在基于这样的特征转换之下会得到更好的结果。

  当使用 full RBF network <script type="math/tex" id="MathJax-Element-373">full\ RBF\ network</script>，也就是将所有的样本点都当做是中心点，来解决以上的二分类问题时，结果如下图，其中最右边的 kNN <script type="math/tex" id="MathJax-Element-374">kNN</script>也是使用所有的样本点作为中心点，只不过在做决策的时候只考虑 k <script type="math/tex" id="MathJax-Element-375">k</script>个。最左侧是在full RBF network<script type="math/tex" id="MathJax-Element-376">full\ RBF\ network</script>上加了正则化项，得到了更加平滑的分类边界。由于在预测的时候， full RBF network <script type="math/tex" id="MathJax-Element-377">full\ RBF\ network</script>这样的模型要考虑所有的资料，所有在实际中通常不是很常用。

  
  

  总结

  本篇主要介绍了 RBF network <script type="math/tex" id="MathJax-Element-259">RBF\ network</script>，其模型由一些中心点 prototype <script type="math/tex" id="MathJax-Element-260">prototype</script>上的径向基函数 RBF <script type="math/tex" id="MathJax-Element-261">RBF</script>构成，这些径向基函数可以高斯函数等等，这些中心点可以是所有的样本点或者是部分具有代表性的样本点。在寻找具有代表性的中心点的过程中，推导出了无监督学习算法， k <script type="math/tex" id="MathJax-Element-262">k</script>-Means<script type="math/tex" id="MathJax-Element-263">Means</script>聚类算法，其优化求解的过程是 alternating optimization <script type="math/tex" id="MathJax-Element-264">alternating\ optimization</script>。当中心点被选取出来之后，构建 RBF network <script type="math/tex" id="MathJax-Element-265">RBF\ network</script>模型就只需要将所有的原始数据经过利用这些中心点结合径向基函数 RBF <script type="math/tex" id="MathJax-Element-266">RBF</script>定义的特征转换得到的新数据上求解一个 linear model <script type="math/tex" id="MathJax-Element-267">linear\ model</script>。最后我们看到这样的算法的表现大多依赖一开始选择的中心点的设置。