混合专家系统（Mixture of Experts）

原理：

混合专家系统（MoE）是一种神经网络，也属于一种combine的模型。适用于数据集中的数据产生方式不同。不同于一般的神经网络的是它根据数据进行分离训练多个模型，各个模型被称为专家，而门控模块用于选择使用哪个专家，模型的实际输出为各个模型的输出与门控模型的权重组合。各个专家模型可采用不同的函数（各种线性或非线性函数）。混合专家系统就是将多个模型整合到一个单独的任务中。

混合专家系统有两种架构：competitive MoE 和cooperative MoE。competitive MoE中数据的局部区域被强制集中在数据的各离散空间，而cooperative MoE没有进行强制限制。

对于较小的数据集，该模型的表现可能不太好，但随着数据集规模的增大，该模型的表现会有明显的提高。

定义X为Nd维输入，y为Nc维输出,K为专家数，$\lambda $为学习率：

$forjin(0...(d-1))andiin(0...(c-1))$:
各专家输出为: $V_{ik}=w_{ik}x$
(其中$w_{ik}$为第k个专家模型对第i列输出的权重，$V_{ik}$为第k个专家对第i列的预测。（$w_{ik}$添加了bias所以输出为d+1维）)

第k个专家输出均值为：

$m_k={\sum }_{i=0}^{c-1}{V}_{ik}$

门限模块输出为：

$g_k=\frac{e^{m_k^T}}{{\sum }_k{e}^{m_k^T}}$
输出$y_i$通过softmax函数转成概率值为： $y_{si}=\frac{e^{y_i}}{{\sum }_i{e}^{y_i}}$

对于Cooperative MoE：

$\Delta w_{ik}=\lambda (y_i-y_{si})g_{k}x$
$\Delta m_k=\lambda (y_i-y_{si})(v_{ik}-y_{si})g_{k}x$
对于Competitive MoE：
$\Delta w_{ik}=\lambda f_k(y_i-y_{ik})x$
$\Delta m_k=\lambda (f_k-g_k)x$
$y_{ik}=\frac{e^{V_{ik}}}{{\sum }_i{e}^{V_{ik}}}$
$f_k=\frac{g_k{e}^{{\sum }_i{y}_{i}log{y}_{ik}}}{{\sum }_l{g}_l{e}^{{\sum }_i{y}_{i}log{y}_{ik}}}$

实验结果：

不同数据集相同k值：

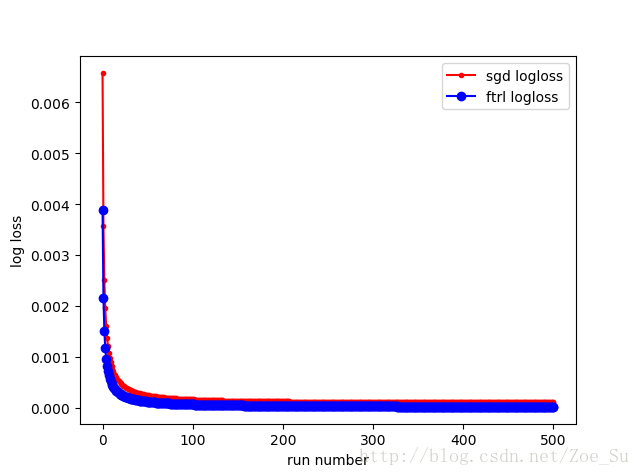
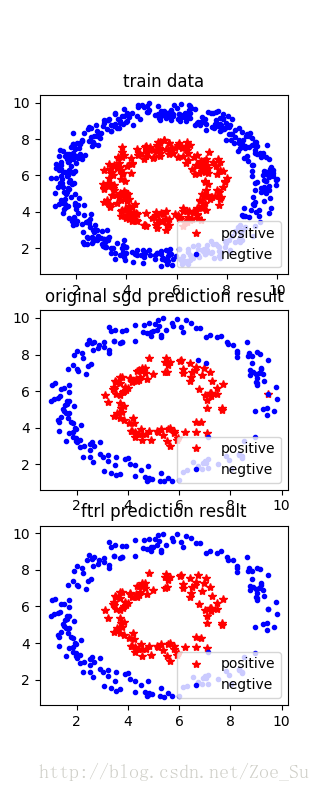
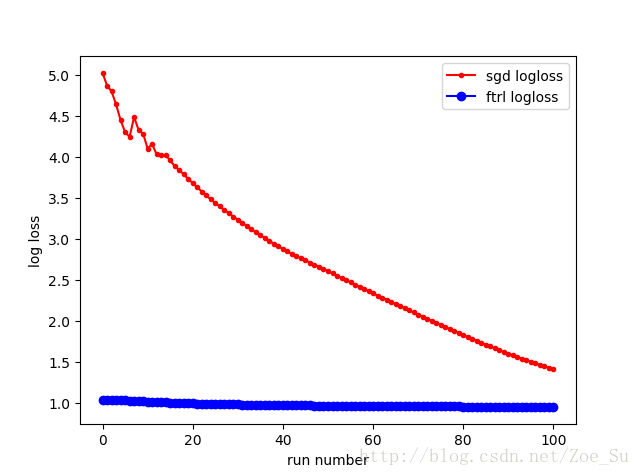
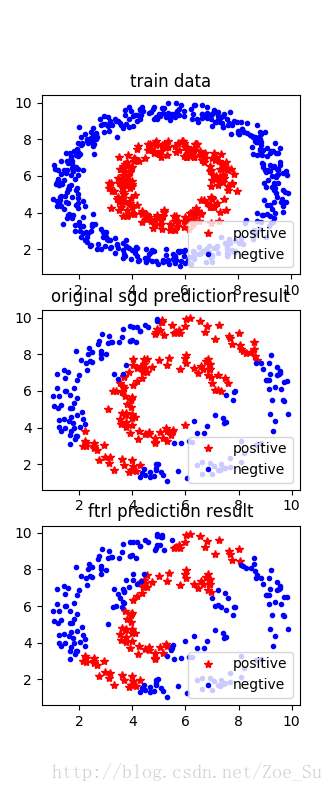
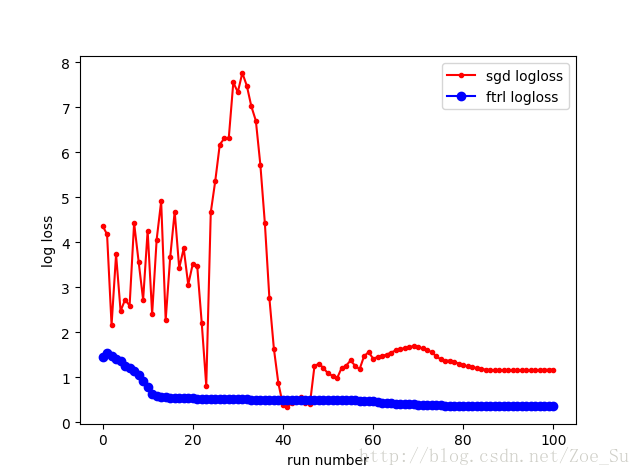
1. k=2使用线性数据集，采用SGD和FTRL两种训练方式，结果如下：
   
   
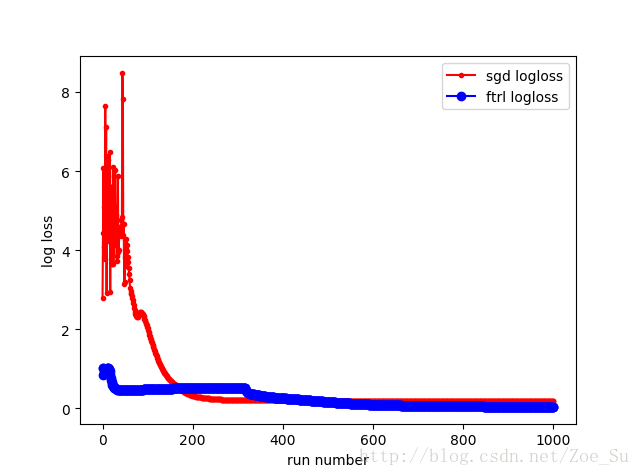
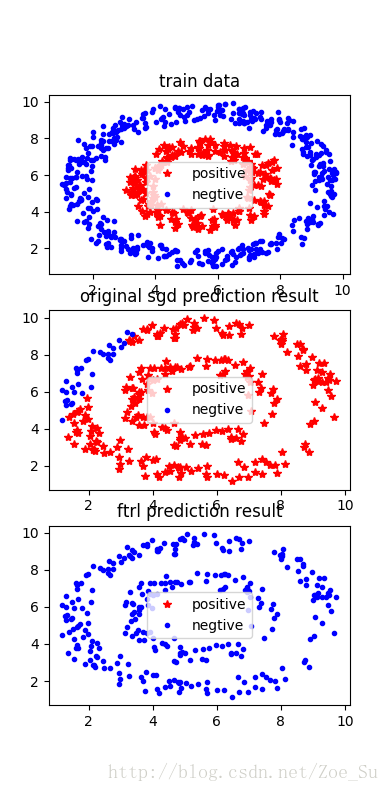
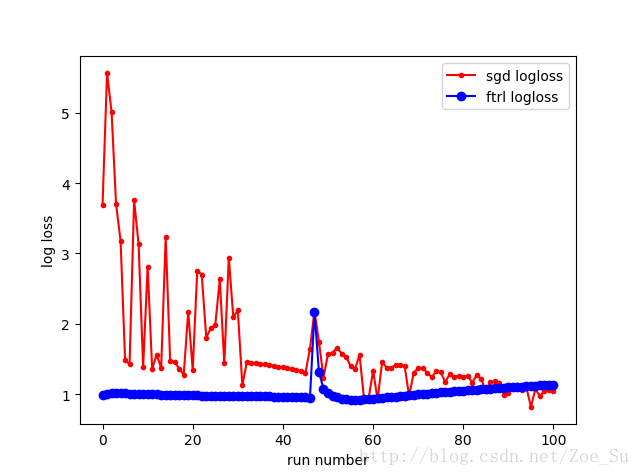
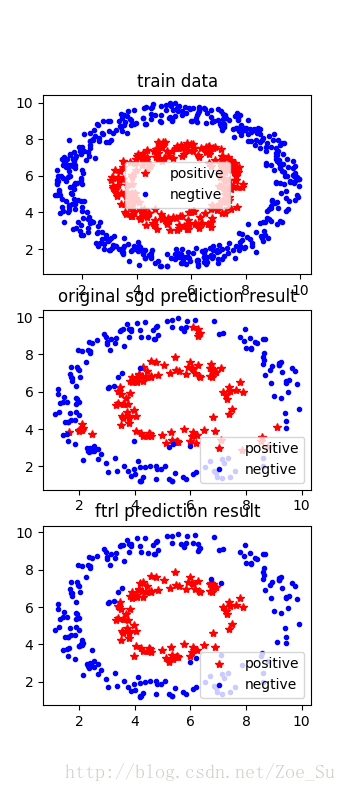
2. k=2使用非线性数据集，采用SGD和FTRL两种训练方式，结果如下：
   
   

相同数据集不同k值：

1. k=1:
   
   
2. k=2:
   
   
3. k=4: