DeepLearning(深度学习)原理与实现(一)
http://blog.csdn.net/marvin521/article/details/8886971 经过三年的狂刷理论,觉得是时候停下来做些有用的东西了,因此决定开博把他们写下来,一是为了整理学过的理论,二是监督自己并和大家分享。先从DeepLearning谈起吧,因为这个有一定的实用性(大家口头传的“和钱靠的很近”),国内各个大牛也都谈了不少,我尽量从其他方面解释一
http://blog.csdn.net/marvin521/article/details/8886971
经过三年的狂刷理论,觉得是时候停下来做些有用的东西了,因此决定开博把他们写下来,一是为了整理学过的理论,二是监督自己并和大家分享。先从DeepLearning谈起吧,因为这个有一定的实用性(大家口头传的“和钱靠的很近” ),国内各个大牛也都谈了不少,我尽量从其他方面解释一下。
),国内各个大牛也都谈了不少,我尽量从其他方面解释一下。
DeepLearning算是多伦多大学Geoffery hinton教授第二春吧,第一春就是传统神经网络,由于传统的多层感知机很容易陷入局部最小,直接用反向传播算法(Back Propagation)求取的分类效果并不如意,原因一是特征是手工的,二就是局部最小问题。而DeepLearning引入了概率图模型里的生成模型,他可以直接自动的从训练集里提取所需要的特征,典型的模型为有限制玻尔兹曼机(Restricted Boltzmann Machines,简称RBM),自动提取的特征解决了手工特征考虑不周的因素,而且很好的初始化了神经网络权重,接着可以采用反向传播算法进行分类,实验得出了很好的效果。 因此DeepLearning被喻为下一代神经网络。今天的话题就来讨论下RBM:
再说RBM之前,我们先提一下基于能量的模型(Engery based model),能量方法来源于热动力学,分子在高温中运动剧烈,能够克服局部约束(分子之间的一些物理约束,比如键值吸引力等),在逐步降到低温时,分子最终会排列出有规律的结构,此时也是低能量状态。受此启发,早期的模拟退火算法就是在高温中试图跳出局部最小。随机场作为物理模型之一,也引入了此方法。在马尔科夫随机场(MRF)中能量模型主要扮演着两个作用:一、全局解的度量(目标函数);二、能量最小时的解(各种变量对应的配置)为目标解,能否把最优解嵌入到能量函数中至关重要,决定着我们具体问题求解的好坏。统计模式识别主要工作之一就是捕获变量之间的相关性,同样能量模型也要捕获变量之间的相关性,变量之间的相关程度决定了能量的高低。把变量的相关关系用图表示出来,并引入概率测度方式就够成了概率图模型的能量模型,其实实际中也可以不用概率表示,比如立体匹配中直接用两个像素点的像素差作为能量,所有像素对之间的能量和最小时的配置即为目标解。RBM作为一种概率图模型,引入概率就是为了方便采样,因为在CD(contrastive divergence)算法中采样部分扮演着模拟求解梯度的角色。
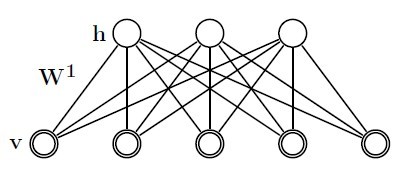
先来看一下RBM模型定义(图一)和能量的定义(公式一):
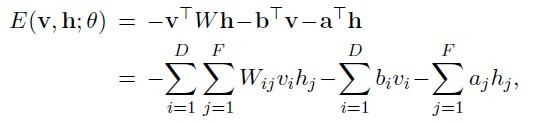
(公式一)
其中v表示实际样本节点,以下叫可视节点,h表示隐藏节点数据,theta={W,b,a},W表示网络权重,b表示可视节点偏移,a表示隐藏节点偏移。这些参数是需要我们求解的,一般开始时我们随机初始化这些参数,对于16*16的二值图像,可视节点有256个,每个节点可能的状态有两个(0,1);隐藏节点的数目由自己制定,每个节点的状态也有两个(0,1)。当每个节点都有一个指定的状态时,此时的RBM有一个对应的能量。此时所有节点对应某个状态的组合成为一个配置。穷举所有配置对应的能量之和就构成了归一化常量Z(配分函数-partition function)。每个配置能量除以常量Z即为当前配置的概率。在一般计算时,为了避免数值计算问题,我们常常引入极家族函数(对数函数和指数函数),那么模型概率定义为(公式二):
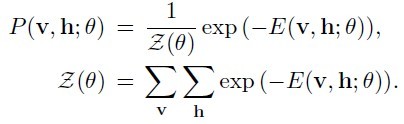
由于RBM是一种生成模型(generative model),我们的目标使得概率p(x)最大时对应的参数theta,常规思路应该使用最大似然法,在求最大似然函数的极值时,我们需要用到梯度法,梯度推导如(图二)所示(大家不要被公式吓倒,CD算法不用它,=、=,只是证明求梯度有点难度):

公式虽然这么写,但是实际中计算归一化分割函数Z时不可取的,因为组合状态是NP-complete的。但是这个公式给出了Contrastive divergence算法的原型(公式三):
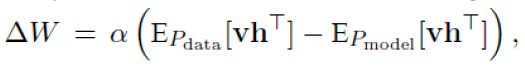
第一项(数据相关期望项):利用可视节点v1乘上权重,然后用sigmoid函数计算出隐藏节点h每个节点的概率,通过此概率对隐藏节点采样,得出隐藏节点状态h1,然后用能量公式计算出所有节点的期望能量(<v1*h1>)作为第一项。
第二项(模型期望项):根据第一项中隐藏节点h1乘上权重,然后用sigmoid函数计算出可视节点v2的概率,在此通过采样得出v2 状态,同样用v2计算出h2的状态,用能量公式计算出所有节点的期望能量(<v2*h2>)。套用上面公式,就可以求出deltaW,
有了类梯度,那么就可以做权重更新咯,迭代就行了,b,a类似求解。
这是用CD算法模拟梯度,关键在于使用什么采样方法,基于MCMC的各种采样方法(如Gibbs,MH,拒绝采样等)请酌情使用,深度理解采样方法有助于我们理解为什么CD可以模拟梯度,用hinton的话来说:这是个惊人的事实。我概括了这么一句话来给我们一个直观的理解:数据期望分布是我们整个数据的分布中心,可以看成最小点,模型期望是采样出来的,具有一定的随机性,分布在中心点周围,二者相减正好可以模拟梯度。其实求解参数theta的方法不止这一种,比如在Russlan的论文中也给出另外一种方法:用随机逼近过程来估计模型期望,用变分方法来估计数据相关期望等。碍于作者水平有限,就不讲了。
另外对DBN这个生成模型(generative model)对参数求导时,得出的结果也和CD公式相似,DBN的训练方法也可以用类似方法训练,具体可参考russlan的代码。
DBM训练方法其实就是层层通过对RBM分别训练。对于russlan论文中提到的其他衍生应用和技巧大家可以根据自己所需详细阅读。比如估计分割函数(Z)是图模型里一个重要的基石部分;autoencoders的神奇作用其实是模拟了神经科学里神经分布式描述,相当于找到了低维流形;深度网络的微调部分(fine-tune),其实通过上述方法做了无监督预训练后,结合标签部分用BP等方法做了权重微更新,值得一提的识别可以用生成模型(generative model),也可以是判别模型(discriminative model),针对具体应用大家可以试着采用不同方法。
我想我要说的基本说完了,整个深度学习除了需要概率图模型和神经网络基础支撑外,也用到了大量的trick。
哦,对了,hinton也说过,神经网络几乎可以模拟现在绝大多数的机器学习方法,包括SVM,Adaboost,当然也包括概率图模型的那一套(其中有结构化学习),这有点把图模型收编的味道,作者视野有限,不敢不认同,也不敢认同。就讲到这里吧,作者写的轻浮一些,公式都是从别人paper上扣下来的,
而且作者水平有限,可能有些会说错,希望大家多多指正。
最后附加一点:概率图模型的能量和概率之间的关系可以参阅gibbs measure和Hammersley–Clifford theorem,他们俩在能量模型到概率之间的转换上扮演着很重要的角色。还有为什么最大化P(x)或者p(v)可以使得能量最小?这个问题一开始我没搞明白,后来一个做事严谨网友(北流浪子)的花了好长时间找到答案,并且无私的与俺分享:对(图二)中的公式(5.7)两边同时取对数得到:lnp(v)=-FreeEnergy(v)-lnZ,这样当p(v)最大时,自由能FreeEnergy(v)最小,而自由能最小决定了系统达到统计平衡,详细可以参考:Gibbs free energy。
参考文献:
[1] Learning Deep Generative models.Ruslan Salakhutdinov
[2] Learning Deep Architectures for AI.Yoshua Bengio
[3] A Tutorial on Energy-Based Models. yann lecun
转载请注明出处:http://blog.csdn.net/cuoqu/article/details/8886971
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容








所有评论(0)