机器学习（十八）——关联规则挖掘

antkillerfarm

26927人浏览 · 2017-03-08 19:50:48

antkillerfarm · 2017-03-08 19:50:48 发布

关联规则挖掘

基本概念（续）

定义一：设 I={i1,i2,…,im} <script type="math/tex" id="MathJax-Element-248">I=\{i_1,i_2,\dots,i_m\}</script>，是m个不同的项目的集合，每个 ik <script type="math/tex" id="MathJax-Element-249">i_k</script>称为一个项目。项目的集合I称为项集。其元素的个数称为项集的长度，长度为k的项集称为k-项集。引例中每个商品就是一个项目，项集为 I={bread,beer,cake,cream,milk,tea} <script type="math/tex" id="MathJax-Element-250">I=\{bread, beer, cake,cream, milk, tea\}</script>，I的长度为6。

定义二：每笔交易T是项集I的一个子集。对应每一个交易有一个唯一标识交易号，记作TID。交易全体构成了交易数据库D， |D| <script type="math/tex" id="MathJax-Element-251">\vert D\vert</script>等于D中交易的个数。引例中包含10笔交易，因此 |D|=10 <script type="math/tex" id="MathJax-Element-252">\vert D\vert=10</script>。

定义三：对于项集X，设定 count(X⊆T) <script type="math/tex" id="MathJax-Element-253">count(X\subseteq T)</script>为交易集D中包含X的交易的数量，则项集X的支持度为：

s u p p o r t (X) = c o u n t ( X \subseteq T ) | D |

引例中 X={bread,milk} <script type="math/tex" id="MathJax-Element-180">X=\{bread, milk\}</script>出现在T1，T2，T5，T9和T10中，所以支持度为0.5。

定义四：最小支持度是项集的最小支持阀值，记为 SUPmin <script type="math/tex" id="MathJax-Element-181">SUP_{min}</script>，代表了用户关心的关联规则的最低重要性。支持度不小于 SUPmin <script type="math/tex" id="MathJax-Element-182">SUP_{min}</script>的项集称为频繁集，长度为k的频繁集称为k-频繁集。如果设定 SUPmin <script type="math/tex" id="MathJax-Element-183">SUP_{min}</script>为0.3，引例中 {bread,milk} <script type="math/tex" id="MathJax-Element-184">\{bread, milk\}</script>的支持度是0.5，所以是2-频繁集。

定义五：关联规则是一个蕴含式：

R ： X \Rightarrow Y

其中 X⊂I <script type="math/tex" id="MathJax-Element-129">X\subset I</script>， Y⊂I <script type="math/tex" id="MathJax-Element-130">Y\subset I</script>，并且 X∩Y=∅ <script type="math/tex" id="MathJax-Element-131">X\cap Y=\varnothing</script>。表示项集X在某一交易中出现，则导致Y以某一概率也会出现。用户关心的关联规则，可以用两个标准来衡量：支持度和可信度。

定义六：关联规则R的支持度是交易集同时包含X和Y的交易数与 |D| <script type="math/tex" id="MathJax-Element-132">\vert D\vert</script>之比。即：

s u p p o r t (X \Rightarrow Y) = c o u n t ( X \cap Y ) | D |

支持度反映了X、Y同时出现的概率。关联规则的支持度等于频繁集的支持度。

定义七：对于关联规则R，可信度是指包含X和Y的交易数与包含X的交易数之比。即：

c o n f i d e n c e (X \Rightarrow Y) = s u p p o r t ( X \Rightarrow Y ) s u p p o r t ( X )

可信度反映了如果交易中包含X，则交易包含Y的概率。一般来说，只有支持度和可信度较高的关联规则才是用户感兴趣的。

定义八：设定关联规则的最小支持度和最小可信度为 SUPmin <script type="math/tex" id="MathJax-Element-95">SUP_{min}</script>和 CONFmin <script type="math/tex" id="MathJax-Element-96">CONF_{min}</script>。规则R的支持度和可信度均不小于 SUPmin <script type="math/tex" id="MathJax-Element-97">SUP_{min}</script>和 CONFmin <script type="math/tex" id="MathJax-Element-98">CONF_{min}</script>，则称为强关联规则。关联规则挖掘的目的就是找出强关联规则，从而指导商家的决策。

这八个定义包含了关联规则相关的几个重要基本概念，关联规则挖掘主要有两个问题：

1.找出交易数据库中所有大于或等于用户指定的最小支持度的频繁项集。

2.利用频繁项集生成所需要的关联规则，根据用户设定的最小可信度筛选出强关联规则。

其中，步骤1是关联规则挖掘算法的难点，下文介绍的Apriori算法和FP-growth算法，都是解决步骤1问题的算法。

参考：

http://blog.csdn.net/OpenNaive/article/details/7047823

Apriori算法

Apriori算法的思路如下：

1.第一次扫描交易数据库D时，产生1-频繁集。在此基础上经过连接、修剪产生2-频繁集。以此类推，直到无法产生更高阶的频繁集为止。

2.在第k次循环中，也就是产生k-频繁集的时候，首先产生k-候选集，k-候选集中每一个项集都是对两个只有一个项不同的属于k-1频繁集的项集连接产生的。

3.k-候选集经过筛选后产生k-频繁集。

从频繁集的定义，我们可以很容易的推导出如下结论：

如果项目集X是频繁集，那么它的非空子集都是频繁集。

如果k-候选集中的项集Y，包含有某个k-1阶子集不属于k-1频繁集，那么Y就不可能是频繁集，应该从候选集中裁剪掉。Apriori算法就是利用了频繁集的这个性质。

参考：

http://zhan.renren.com/dmeryuyang?gid=3602888498023976650&checked=true

http://blog.csdn.net/lizhengnanhua/article/details/9061755

FP-growth算法

Aprori算法利用频繁集的两个特性，过滤了很多无关的集合，效率提高不少，但是我们发现Apriori算法是一个候选消除算法，每一次消除都需要扫描一次所有数据记录，造成整个算法在面临大数据集时显得无能为力。

FP-Growth算法是韩家炜等人在2000年提出的关联分析算法。它通过构造一个树结构来压缩数据记录，使得挖掘频繁项集只需要扫描两次数据记录，而且该算法不需要生成候选集合，所以效率会比较高。

注：韩家炜，中国科学技术大学本科（1979）+中科院硕士+威斯康辛大学博士（1985）。美国伊利诺伊大学香槟分校计算机系教授，IEEE和ACM院士。

FpGrowth算法的平均效率远高于Apriori算法，但是它并不能保证高效率，它的效率依赖于数据集，当数据集中的频繁项集的没有公共项时，所有的项集都挂在根结点上，不能实现压缩存储，而且Fptree还需要其他的开销，需要存储空间更大，使用FpGrowth算法前，对数据分析一下，看是否适合用FpGrowth算法。

参考：

http://www.cnblogs.com/fengfenggirl/p/associate_fpgowth.html

幸存者偏差

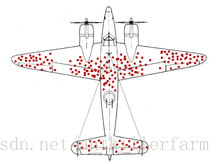
二战期间，盟军需要对战斗机进行装甲加厚，以提高生还率，但由于军费有限，只能进行局部升级。那么问题来了，究竟哪个部位最关键，最值得把装甲加厚来抵御敌方炮火呢？人们众口不一，最后一致决定采用统计调查的方式来解决，即：仔细检查每一驾战斗机返回时受到的损伤程度，计算出飞机整体的受弹状况，然后根据大数据分析决定。

不久，统计数据很快出炉：盟军飞机普遍受弹最严重的地方是机翼，有的几乎被打成了筛子；相反，受弹最轻的地方是驾驶舱及尾部发动机，许多飞机的驾驶舱甚至连擦伤都没有。

这里写图片描述

正当所有人拿着这份确凿无疑的报告准备给机翼加厚装甲时，统计学家Abraham Wald阻拦了他们，同时提出了一个完全相反的方案：加厚驾驶舱与尾部。理由非常简单：这两个位置中弹的飞机，都没有回来。换言之，它们是一份沉默的数据——“死人不会说话”。

最后，盟军高层纷纷听取了这个建议，加固了驾驶舱与尾部，果然空中战场局势得以好转，驾驶员生还率也大大提高。事实证明，这是一个无比英明的措施。

这个事例也被称作“幸存者偏差”（Survivorship bias）。它是一种典型的由于模型不当，导致的“数据说谎”。

注：Abraham Wald，1902～1950，生于奥匈帝国，维也纳大学博士。1938年为躲避纳粹，移民美国，哥伦比亚大学教授。Herman Chernoff的导师。其子Robert M. Wald，为著名理论物理学家，芝加哥大学教授，黑洞理论的提出者之一。

关联规则评价

“数据说谎”的问题很普遍。再看这样一个例子，我们分析一个购物篮数据中购买游戏光碟和购买影片光碟之间的关联关系。交易数据集共有10,000条记录，如表1所示：

表1	买游戏	不买游戏	行总计
买影片	4000	3500	7500
不买影片	2000	500	2500
列总计	6000	4000	10000

假设我们设置得最小支持度为30%，最小自信度为60%。从上面的表中，可以得到：

s u p p o r t (买 游 戏 光 碟 \to 买 影 片 光 碟) = 4000 / 10000 = 40 %

c o n f i d e n c e (买 游 戏 光 碟 \to 买 影 片 光 碟) = 4000 / 6000 = 66 %

这条规则的支持度和自信度都满足要求，因此我们很兴奋，我们找到了一条强规则，于是我们建议超市把影片光碟和游戏光碟放在一起，可以提高销量。

可是我们想想，一个喜欢的玩游戏的人会有时间看影片么，这个规则是不是有问题，事实上这条规则误导了我们。在整个数据集中买影片光碟的概率p(买影片)=7500/10000=75%，而买游戏的人也买影片的概率只有66%，66%<75%恰恰说明了买游戏光碟抑制了影片光碟的购买，也就是说买了游戏光碟的人更倾向于不买影片光碟，这才是符合现实的。

从上面的例子我们看到，支持度和自信度并不总能成功滤掉那些我们不感兴趣的规则，因此我们需要一些新的评价标准，下面介绍几种评价标准：

确信度

Conviction的定义如下：

c o n v (X \Rightarrow Y) = 1 - s u p p ( Y ) 1 - c o n f ( X \Rightarrow Y )

它的值越大，表明X、Y的独立性越小。

卡方系数

卡方系数是与卡方分布有关的一个指标。参见：

https://en.wikipedia.org/wiki/Chi-squared_distribution

χ 2 = \sum i = 1 n ( O i - E i ) 2 E i

注：上式最早是Pearson给出的。

公式中的 Oi <script type="math/tex" id="MathJax-Element-65">O_i</script>表示数据的实际值， Ei <script type="math/tex" id="MathJax-Element-66">E_i</script>表示期望值，不理解没关系，我们看一个例子就明白了。

表2	买游戏	不买游戏	行总计
买影片	4000(4500)	3500(3000)	7500
不买影片	2000(1500)	500(1000)	2500
列总计	6000	4000	10000

表2的括号中表示的是期望值。以第1行第1列的4500为例，其计算方法为：7500×6000/10000。

经计算可得表2的卡方系数为555.6。基于置信水平和自由度 (r−1)∗(c−1)=(行数−1)∗(列数−1)=1 <script type="math/tex" id="MathJax-Element-67">(r-1)*(c-1)=(行数-1)*(列数-1)=1</script>，查表得到自信度为(1-0.001)的值为6.63。