特征选择和提取(一)
特征选择和提取是模式识别中的一个关键问题:前面讨论分类器设计的时候,一直假定已给出了特征向量维数确定的样本集,其中各样本的每一维都是该样本的一个特征;这些特征的选择是很重要的,它强烈地影响到分类器的设计及其性能;假若对不同的类别,这些特征的差别很大,则比较容易设计出具有较好性能的分类器。特征选择和提取是构造模式识别系统时的一个重要课题:在很多实际问题中,往往不容易找到那些最重要的特征,或受客观
特征选择和提取是构造模式识别系统时的一个重要课题:在很多实际问题中,往往不容易找到那些最重要的特征,或受客观条件的限制,不能对它们进行有效的测量;因此在测量时,由于人们心理上的作用,只要条件许可总希望把特征取得多一些;另外,由于客观上的需要,为了突出某些有用信息,抑制无用信息,有意加上一些比值、指数或对数等组合计算特征;如果将数目很多的测量值不做分析,全部直接用作分类特征,不但耗时,而且会影响到分类的效果,产生“特征维数灾难”问题。
为了设计出效果好的分类器,通常需要对原始的测量值集合进行分析,经过选择或变换处理,组成有效的识别特征;在保证一定分类精度的前提下,减少特征维数,即进行“降维”处理,使分类器实现快速、准确和高效的分类。为达到上述目的,关键是所提供的识别特征应具有很好的可分性,使分类器容易判别。为此,需对特征进行选择。(1)应去掉模棱两可、不易判别的特征;(2)所提供的特征不要重复,即去掉那些相关性强且没有增加更多分类信息的特征。
特征选择:
特征选择就是从n个度量值集合{x1, x2,…, xn}中,按某一准则选取出供分类用的子集,作为降维(m维,m<n)的分类特征;
所谓特征提取,就是使(x1, x2,…, xn)通过某种变换,产生m个特征(y1, y2,…, ym) (m<n) ,作为新的分类特征(或称为二次特征);
其目的都是为了在尽可能保留识别信息的前提下,降低特征空间的维数,已达到有效的分类。
模式类别可分性的测度:
点到点之间的距离
在n维空间中,a与b两点之间的欧氏距离为:D(a, b) = || a – b ||;写成距离平方:

点到点集之间的距离
在n维空间中,点x到点a(i)之间的距离平方为:
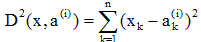
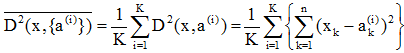
n维空间中同一类内各模式样本点集{a(i)}i=1,2,…,K,其内部各点的均方距离为 ,其中 ,即:



 为{a(i)}在第k个分量方向上的均值。
为{a(i)}在第k个分量方向上的均值。
考虑一类内模式点集 ,其类内散布矩阵为:


类间距离和类间散布矩阵
在考虑有两个以上的类别,如集合{a(i)}和{b(j)}时,类间距离对类别的可分性起着重要作用,此时应计算:


 为m1和m2的第k个分量,n为维数。
为m1和m2的第k个分量,n为维数。写成矩阵形式:
为两类模式的类间散布矩阵。
对三个以上的类别,类间散布矩阵常写成:


多类模式集散布矩阵
多类情况的类内散布矩阵,可写成各类的类内散布矩阵的先验概率的加权和,即:

有时,用多类模式总体分布的散布矩阵来反映其可分性,即:

可以证明:St = Sw + Sb,即总体散布矩阵是各类类内散布矩阵与类间散布矩阵之和。
对于独立特征的选择准则
类别可分性准则应具有这样的特点,即不同类别模式特征的均值向量之间的距离应最大,而属于同一类的模式特征,其方差之
和应最小。假设各原始特征测量值是统计独立的,此时,只需对训练样本的n个测量值独立地进行分析,从中选出m个最好的作为分
类特征即可。
对于ωi和ωj两类训练样本的特征选择
例:对于ωi和ωj两类训练样本,假设其均值向量为mi和mj,其k维方向的分量为mik和mjk,方差为
函数:
则GK为正值。GK值越大,表示测度值的第k个分量对分离ωi和ωj两类越有效。将{GK, k=1,2,…,n}按大小排队,选出最大的m
个对应的测度值作为分类特征,即达到特征选择的目的。
(a) 中特征xk的分布有很好的可分性,通过它足以分离wi和wj两种类别;
(b) 中的特征分布有很大的重叠,单靠xk达不到较好的分类,需要增加其它特征;
(c) 中的wi类特征xk的分布有两个最大值,虽然它与wj的分布没有重叠,但计算Gk约等于0,此时再利用Gk作为可分性准则已不合适。

类内:


行列式形式:


 的特征值。使J1或J2最大的子集可作为选择的分类特征。类内、类间的散布矩阵Sw和Sb类间离散度越大
的特征值。使J1或J2最大的子集可作为选择的分类特征。类内、类间的散布矩阵Sw和Sb类间离散度越大
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容










所有评论(0)