背景

在自然语言的处理或者语音识别方面，我们可以跟编码解码进行类比，比如说从汉语到英语的翻译，说话者讲的是汉语，从汉语到英语的翻译过程可以理解为编码。翻译成英文的效果根据上文中统计语言模型提到的概率来评价，概率越大，翻译的效果越好。所以只要找到条件概率最大即为翻译后的结果。公式表示如下：

<script type="math/tex; mode=display" id="MathJax-Element-1">s_1,s_2,s_3,...= Max_{all \ s_1,s_2,s_3... }P(s_1,s_2,s_3...|o_1,o_2,o_3...)</script>
利用贝叶斯公式：
<script type="math/tex; mode=display" id="MathJax-Element-2">Max_{all \ s_1,s_2,s_3... }P(s_1,s_2,s_3...|o_1,o_2,o_3...)=Max_{all \ s_1,s_2,s_3... }\frac{P(o_1,o_2,o_3,...|s_1,s_2,s_3,...)P(s_1,s_2,s_3,...)}{P(o_1,o_2,o_3,...)}</script>
其中P(o1,o2,o3,...|s1,s2,s3,...)<script type="math/tex" id="MathJax-Element-3">P(o_1,o_2,o_3,...|s_1,s_2,s_3,...)</script>表示信息s1,s2,s3,...<script type="math/tex" id="MathJax-Element-4">s_1,s_2,s_3,...</script>在翻译前是o1,o2,o3,...<script type="math/tex" id="MathJax-Element-5">o_1,o_2,o_3,...</script>的可能性。P(s1,s2,s3,...)<script type="math/tex" id="MathJax-Element-6">P(s_1,s_2,s_3,...)</script>表示s1,s2,s3,...<script type="math/tex" id="MathJax-Element-7">s_1,s_2,s_3,...</script>是一个合乎情理的句子的可能性。而P(o1,o2,o3,...)<script type="math/tex" id="MathJax-Element-8">P(o_1,o_2,o_3,...)</script>表示要翻译o1,o2,o3,...<script type="math/tex" id="MathJax-Element-9">o_1,o_2,o_3,...</script>的可能性。
因为一般来说P(o1,o2,o3,...)<script type="math/tex" id="MathJax-Element-10">P(o_1,o_2,o_3,...)</script>的可能性是固定的，所以上面的式子可以简化为：
<script type="math/tex; mode=display" id="MathJax-Element-11">Max_{all \ s_1,s_2,s_3... }P(o_1,o_2,o_3,...|s_1,s_2,s_3,...)P(s_1,s_2,s_3,...)</script>

隐含马尔科夫模型

针对上面提出的公式，其实可以使用隐含马尔科夫模型来估计。

马尔科夫链

举个例子来说，长江水面高度的监控其实是一件很重要的事情，长江水面的高度可能跟前些天的水面高度以及是否下雨等天气相关。所以要预测长江水面高度是一件很复杂的事情。马尔科夫为了简化问题，提出了一种假设—-假设当前的状态只与它的前一个状态相关，即P(st|s1,s2,s3,...st−1)=P(st|st−1)<script type="math/tex" id="MathJax-Element-12">P(s_t|s_1,s_2,s_3,...s_{t-1})=P(s_t|s_{t-1})</script>.
这个假设就是马尔科夫假设。而符合这个假设的随机过程称为马尔科夫过程，也称为马尔科夫链。

举例

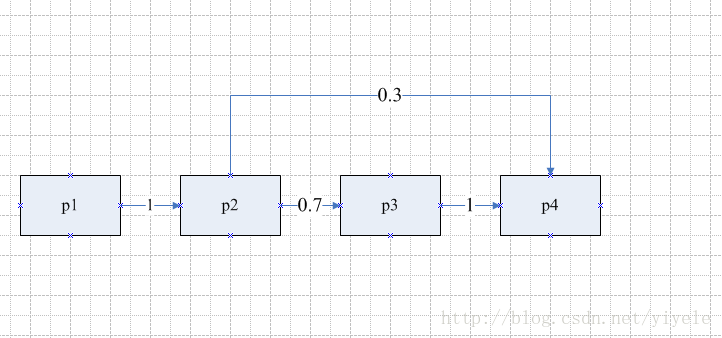
如上图所示，表示一个简单的离散马尔科夫链。其中四个长方形表示四个状态，每条边表示状态转换，边上的权值表示转换概率。从上图可知从p1到p2的转换概率为1，即P(st+1=p2|st=p1)=1<script type="math/tex" id="MathJax-Element-13">P(s_{t+1}=p2|s_t=p1)=1</script>。p2到p3的概率为0.7，即P(st+1=p3|st=p2)=0.7<script type="math/tex" id="MathJax-Element-14">P(s_{t+1}=p3|s_t=p2)=0.7</script>。

综述（计算转移概率）

因为马尔科夫链中每个状态只与前一个状态相关，所以我们在看到一个马尔科夫链时，可以根据统计的方式来计算概率，比如说P(st+1|st)<script type="math/tex" id="MathJax-Element-50">P(s_{t+1}|s_t)</script>，如果计算这个概率我们只需要统计st<script type="math/tex" id="MathJax-Element-51">s_t</script>出现的次数nt<script type="math/tex" id="MathJax-Element-52">n_t</script>，以及从st<script type="math/tex" id="MathJax-Element-53">s_t</script>转换到st+1<script type="math/tex" id="MathJax-Element-54">s_{t+1}</script>的次数nt,t+1<script type="math/tex" id="MathJax-Element-55">n_{t,t+1}</script>，最终的结果为

<script type="math/tex; mode=display" id="MathJax-Element-56">P(s_{t+1}|s_t)=\frac{n_t}{n_{t,t+1}}</script>

隐含马尔科夫模型

隐含马尔科夫模型是马尔科夫模型的拓展，即任意时刻的状态是不可观测的。所以我们无法直接观测一个马尔科夫链，以及根据根据马尔科夫链计算后续的转移概率。但是隐含马尔科夫模型在任意时刻会输出一个状态ot<script type="math/tex" id="MathJax-Element-478">o_t</script>，且这个状态只与st<script type="math/tex" id="MathJax-Element-479">s_t</script>相关，这个被称为独立输出假设。具体如下图所示：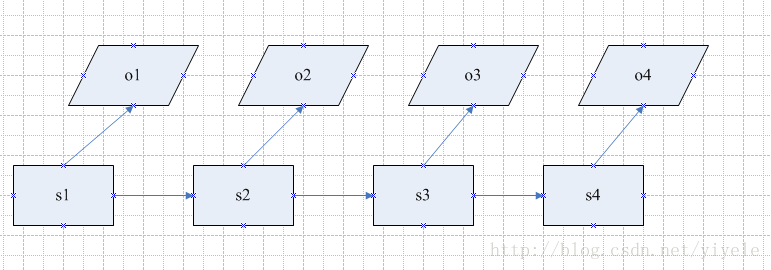

基于马尔科夫假设和独立输出假设，可以计算出某个特定的状态序列s1,s2,s3...<script type="math/tex" id="MathJax-Element-480">s_1,s_2,s_3...</script>产生输出状态o1,o2,o3...<script type="math/tex" id="MathJax-Element-481">o_1,o_2,o_3...</script>的概率：

<script type="math/tex; mode=display" id="MathJax-Element-482">P(s_1,s_2,s_3...,o_1,o_2,o_3...)=\prod_{t}P(s_t|s_{t-1})P(o_t|s_t)</script>

最后

在一开始提出的式子Maxall s1,s2,s3...P(o1,o2,o3,...|s1,s2,s3,...)P(s1,s2,s3,...)<script type="math/tex" id="MathJax-Element-455">Max_{all \ s_1,s_2,s_3... }P(o_1,o_2,o_3,...|s_1,s_2,s_3,...)P(s_1,s_2,s_3,...)</script>中，根据上面的介绍可得：

<script type="math/tex; mode=display" id="MathJax-Element-456">P(o_1,o_2,o_3,...|s_1,s_2,s_3,...)=\prod_{t}P(o_t|s_t)</script>
<script type="math/tex; mode=display" id="MathJax-Element-457">P(s_1,s_2,s_3,...)=\prod_{t}P(s_t|s_{t-1})</script>
最后至于最大值的求解可以使用维特比算法。