图机器学习——2.1 节点嵌入：基于随机游走

嵌入（embedding）方法是目前文本分析，知识图谱相关中非常常见的一种算法。其为表示学习的一类方法，可以自动地从数据中学习“有用”的特征，并可以直接用于后续的具体任务。后面学习的相关嵌入学习均为表示学习中的内容。节点嵌入关于图的一些信息如何能够转化为计算机可以识别的语言呢？通常的方法也是进行嵌入（embedding）。在此之前，我们已经学习了双曲嵌入：双曲嵌入深度学习双曲嵌入论文与代码实现——

Kanny广小隶

3233人浏览 · 2021-11-22 12:18:26

Kanny广小隶 · 2021-11-22 12:18:26 发布

嵌入（embedding）方法是目前文本分析，知识图谱相关中非常常见的一种算法。其为表示学习的一类方法，可以自动地从数据中学习“有用”的特征，并可以直接用于后续的具体任务。后面学习的相关嵌入学习均为表示学习中的内容。

节点嵌入

关于图的一些信息如何能够转化为计算机可以识别的语言呢？通常的方法也是进行嵌入（embedding）。在此之前，我们已经学习了双曲嵌入：

其将图结构嵌入到双曲空间中而后根据双曲距离进行embedding的训练。这种做法其实是一种比较新的方法，而在此之前的那些传统的节点嵌入方法都没有进行学习。因此，基于双曲空间的节点嵌入方法，本系列博客不再进行具体介绍。

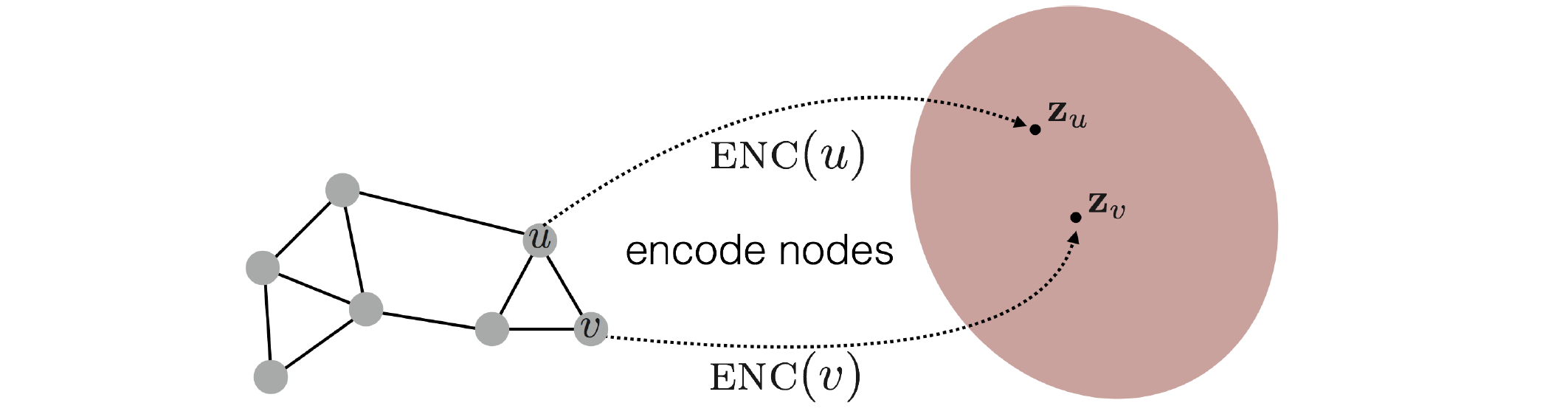
总体而言，节点的嵌入通常采取编码-解码结构进行训练。编码示意图如下：

总体的编解码核心思路如下：

编码器ENC定义了一个从图中的节点 $u, v$ 到一个空间中的嵌入 $\mathbf{z}_{u}, \mathbf{z}_{v}$ 的映射；

$\text{ENC}(v) = \mathbf{z}_{v}$

定义一个节点相似度函数(即原始网络中的相似度度量, similarity)；
解码器DEC定义一个从嵌入到相似度评分的映射；
通过编码器优化参数，使得下式左右两边尽可能接近：
$\operatorname{similarity}(u, v) \approx \mathbf{z}_{v}^{\mathrm{T}} \mathbf{z}_{u}$

左式表示原始网络中节点 $u, v$ 的相似度；右式表示解码后的相似度评分。

基于随机游走的方法

1. DeepWalk

DeepWalk方法受到 word2vec 的启发，首先选择某一特定点为起始点，做随机游走得到点的序列，然后将这个得到的序列视为句子，用 word2vec 来学习，得到该点的表示向量。DeepWalk通过随机游走去可以获图中点的局部上下文信息，因此学到的表示向量反映的是该点在图中的局部结构，两个点在图中共有的邻近点（或者高阶邻近点）越多，则对应的两个向量之间的距离就越短。

图上的随机游走：给定一个图和一个起点，我们随机选择它的一个邻居，并移动到这个邻居；接着我们随机选择这一点的一个邻居，然后继续移动到它，重复这个操作。以这种方式访问的(随机)节点序列是图上的一个随机游走。

我们的目标是学习到一个映射 $\rightarrow \mathbb{R}^{d}:$ $f(u)=\mathbf{z}_{u}$

Log-likelihood 定义如下：
$\max _{f} \sum_{u \in V} \log \mathrm{P}\left(N_{\mathrm{R}}(u) \mid \mathbf{z}_{u}\right)$

$N_{R}(u)$ 是从节点 $u$ 出发，通过游走策略 $R$ 所能到达的节点。给定节点 $u$ ，我们想要学习的特征表示是节点对随机游走邻居 $N_{R}(u)$ 的预测。直觉上，我们的优化目的是要使得从 $u$ 出发，尽可能使预测到邻居的概率更大，然后遍历所有的节点对总体进行优化。

下面为具体的算法过程：

从图的每个节点 $u$ 开始，使用一些随机游走策略 $R$ 进行短的固定长度随机游走；
对于每个节点 $u$ 计算 $N_{R}(u)$ ，即从 $u$ 开始游走路过的节点集合；
给定节点 $u$ ，预测其邻居结点 $N_{\mathrm{R}}(u)$ ，通过最大化似然函数（下式）最优化嵌入：

$\max _{f} \sum_{u \in V} \log P\left(N_{\mathrm{R}}(u) \mid \mathbf{z}_{u}\right)$

上述的式子其实等价于下面的损失函数：

$\mathcal{L}=\sum_{u \in V} \sum_{v \in N_{R}(u)}-\log \left(P\left(v \mid \mathbf{z}_{u}\right)\right)$

我们用softmax函数来参数化 $P\left(v \mid \mathbf{z}_{u}\right)$ ：

$P\left(v \mid \mathbf{z}_{u}\right)=\frac{\exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)}{\sum_{n \in V} \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)}$

因此实际的损失函数为：
$\mathcal{L}=\sum_{u \in V} \sum_{v \in N_{R}(u)} -\log \left(\frac{\exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)}{\sum_{n \in V} \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)}\right)$

但注意到上式的分母 $\sum_{n \in V} \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)$ 需要遍历网络的所有节点，计算量非常大。为了减少算法复杂度，可以使用负采样策略（Negative sampling，REF: https://arxiv.org/pdf/1402.3722.pdf）。

$\begin{aligned} &\log \left(\frac{\exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)}{\sum_{n \in V} \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)}\right)\\ &\approx \log \left(\sigma\left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)\right)-\sum_{i=1}^{k} \log \left(\sigma\left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n_{i}}\right)\right), n_{i} \sim P_{V} \end{aligned}$

其中， $P_v$ 为节点随机分布， $\sigma(t)=\frac{1}{1+e^{-t}}$ 。

这样只要随机选取 $k$ 个“负样本”，即可快速近似到原式，在实际的操作中，通常选自5-20之间的数。

最终优化时用随机梯度下降的方法进行优化即可。

至此，整个基于随机游走的嵌入方法已经基本阐述完了。但有一个关键问题是：我们应该使用什么策略来进行随机游走？

通常最简单的做法是直接固定游走长度，每个邻接节点都是等概率进行游走。但这样的游走其实并不高效，基于这个原因，node2vec方法被提出。

2. node2vec

与DeepWalk相似，node2vec通过最大化随机游走得到的序列中的节点出现的概率来保持节点之间的高阶邻近性。与DeepWalk的最大区别在于，node2vec采用有偏随机游走，在广度优先（bfs）和深度优先（dfs）图搜索之间进行权衡，从而产生比DeepWalk更高质量和更多信息量的嵌入。

对于节点 $u$ ，node2vec发展了一个有偏的二阶随机游走策略 $R$ 来生成网络的领域 $N_{R}(u)$ 。核心思想为：使用一个灵活、有偏差的随机游走，其可以在网络的局部和全局视角之间进行权衡。

为此，我们定义节点 $u$ 的两种邻居 $N_R(u)$ 。如上图所示， $N_{B F S}(u)=\left\{s_{1}, s_{2}, s_{3}\right\}$ 为局部微观视角下的游走； $N_{D F S}(u)=\left\{s_{4}, s_{5}, s_{6}\right\}$ 为全局宏观视角下的游走。