机器人的位置（Position）和姿态（Pose）常常统称为位姿。位姿描述是表达机器人的线速度、角速度、力和力矩的基础，而坐标变换是研究不同坐标系中的机器人位姿关系的重要途径。

2.1 位姿的数学描述

2.1.1 位置描述

一个坐标系在空间中的位置可以通过一个三维向量来表示，如图 2.1 所示，用三个相互正交带有箭头的单位矢量来表示一个参考坐标系 $A$，通过一个矢量表示参考坐标系中的一个点 ${}^{A}P$ ，可以由一个$3\times 1$向量表示：

$${}^{A}P=[p_x,p_y,p_z{]}^T\text{\hspace{1em}(2-1)}$$

其中，$p_x,p_y,p_z$分别为空间点在参考坐标系 $A$ 的 X,Y,Z 坐标轴的投影。

图 2.1 位置描述

2.1.2 姿态描述

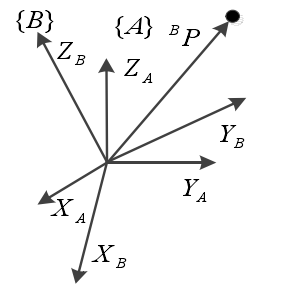
对于空间中的一个点可以用位置矢量描述，但是对于空间中的一个物体，仅仅使用位置描述显然是不够的，所以还需要引入姿态描述。如图 2.2 所示，为了描述物体的姿态，我们通过在物体上固定一个坐标系$B$，用坐标系$B$相对于坐标系 $A$的关系描述物体的姿态。通过$X_B$,$Y_B$和$Z_B$和表示坐标系主轴方向的单位矢量，其在参考坐标系中的表示可以被写成 ${}^A{X}_B$、${}^A{Y}_B$ 和 ${}^A{Z}_B$。通过一个 3×3 的矩阵来表示坐标系$B$相对于坐标系$A$的姿态描述。

$${}_B^{A}R={[}^A{X}_B,{}^A{Y}_B,{}^A{Z}_B]=\left[\begin{array}{ccc}{X}_B{X}_A& Y_B{X}_A& Z_B{X}_A\\ & & \\ X_B{Y}_A& Y_B{Y}_A& Z_B{Y}_A\\ & & \\ X_B{Z}_A& Y_B{Z}_A& Z_B{Z}_A\end{array}\right]\text{\hspace{1em}(2-2)}$$

图 2.2 姿态描述

分析式(2-2)可以发现，矩阵 ${}_B^{A}R$的行是坐标系$A$的单位矢量在坐标系$B$中的表示形式，则有以下式子成立：

$${}_B^{A}R={[}^A{X}_B,{}^A{Y}_B,{}^A{Z}_B]=\left[\begin{array}{c}{}^B{X}_A\\ \\ {}^B{Y}_A\\ \\ {}^B{Z}_A\end{array}\right]\Rightarrow {}_B^A{R}^T={}_A^{B}R\text{\hspace{1em}(2-3)}$$

需要注意的是，旋转矩阵是一种特殊的每列相互正交的单位矩阵，其行列式恒等于1，我们称之为标准正交矩阵。而对于任何一个正交矩阵$R$存在一个反对称矩阵$S$，满足以下条件：

$$R=(I_3-S{)}^{-1}(I_3+S)\text{\hspace{1em}(2-4)}$$

其中，$I_3$为 3×3 的单位矩阵，可以由3个参数 $(s_x,s_y,s_z)$表示。

因此旋转矩阵可以由3个参数即可确定，根据《机器人学导论》所述，常采用的方法有$XYZ$固定角，$ZYX$欧拉角，$ZYZ$欧拉角。由于后续运动学只涉及到了$XYZ$固定角，以下只对$XYZ$固定角进行介绍。

如图 2.3 所示，以坐标系$B$表示空间连杆对应的坐标系，以固定坐标系$A$为参考坐标系，将坐标系$B$和坐标系$A$重合，依次将坐标系$B$绕$X_A$按右手螺旋法则旋转$\gamma$角，再绕$Y_A$按右手螺旋法则旋转$\beta$角，最后绕$Z_A$按右手螺旋法则旋转$\alpha$角。

图 2.3 固定角旋转示意图

每次旋转都是绕着固定参考坐标系 $A$ 旋转，通常用横滚角 (roll)，俯仰角 (pitch) 和偏转角 (yaw) 分别表示$\gamma$，$\beta$和 $\alpha$，简称 RPY 角。则用 RPY 角表示的旋转矩阵为：

在运动学应用中，姿态信息通常需要在旋转矩阵与角之间进行相互转换，如在机械臂正运动学分析过程中，需要考虑其逆问题，即从旋转矩阵等价推导出 RPY 表示的 XYZ 固定角；而在机械臂逆运动学分析过程中，只需按照式(2-5)即可将表示法的姿态信息转换为旋转矩阵。下面推导其逆问题，即已知旋转矩阵推出 RPY 表示的 XYZ 固定角。令

$${}_B^A{R}_{XYZ}(\gamma ,\beta ,\alpha )=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ & & \\ r_{21}& r_{22}& r_{23}\\ & & \\ r_{31}& r_{32}& r_{33}\end{array}\right]\text{\hspace{1em}(2-6)}$$

结合式(2-5)，通过计算$r_{11}$和$r_{21}$的平方和再开方根，即可求得$cos\beta$，当$c\beta \ne 0$时，再用$-r_{31}$除以 $c\beta$，可得$tan\beta$，最后求反正切即可求得$\beta$：

$$\beta =atan2(-r_{31},\sqrt{r_{11}^2+r_{21}^2})\text{\hspace{1em}(2-7)}$$

当 $c\beta \ne 0$ 时，利用 $r_{21}/c\beta$ 除以$r_{11}/c\beta$再求反正切得到$\alpha$：

$$\alpha =atan2(r_{21}/c\beta ，r_{11}/c\beta )\text{\hspace{1em}(2-8)}$$

当 $c\beta \ne 0$ 时，利用 $r_{32}/c\beta$ 除以 $r_{33}/c\beta$ 再求反正切得到$\gamma$：

$$\gamma =atan2(r_{32}/c\beta ，r_{33}/c\beta )\text{\hspace{1em}(2-9)}$$

当 $c\beta =0$ 时，即 $\beta =\pm 90^o$ 时，此时只能求出和的和或者差，一般 $\alpha =0$ 令，可解得：

$$\beta =\pm 90,\alpha =0,\gamma =\pm atan2(r_{12},r_{22})\text{\hspace{1em}(2-10)}$$

以上式子中，$atan2$ 是双参数四象限反正切函数，其值域在$(-\pi ,\pi ]$；而 $atan$ 是单参数反正切函数，其值域在$(-\pi /2,\pi /2]$。$atan2$ 取值范围更大，实际应用中可能存在两种解，根据需要取舍，在一些编程语言库中也有对应的预定义，方便嵌入式代码实现。

(3) 位姿描述

要完整描述空间中的物体所需的信息需要位置和姿态组合的形式来表示，即位姿。空间中物体相对参考坐标系的位姿描述可以用式(2-11)表示：

$$B={[}_B^{A}R{,}^A{P}_{BORG}]\text{\hspace{1em}(2-11)}$$

其中，旋转矩阵 ${}_B^{A}R$ 表示物体坐标系 $B$ 相对于参考坐标系 $A$ 的姿态信息，${}^A{P}_{BORG}$ 表示物体坐标系 $B$ 相对于参考坐标系 $A$ 的位置信息。

2.2 坐标变换

由上述位姿描述可知，物体的位置和姿态是根据参考坐标系唯一确定的，当在不同参考坐标系进行同一物体位姿描述时，位姿表示也会随之发生变化。因此需要用到坐标变换将物体在不同参考坐标系下的描述关联起来。不同坐标系之间的坐标变换包括：平移变换、旋转变换以及复合变换。

2.2.1 平移变换

平移变换指物体在空间中保持姿态不变的运动。如图2.4 所示，坐标系 $A$ 和坐标系 $B$ 的姿态相同，不同的是只发生了平移。$P$点在坐标系$B$的位置用矢量${}^{B}P$表示，在坐标系$A$的位置用矢量${}^{A}P$表示，$B$的原点相对于$A$的位置用矢量${}^A{P}_{BORG}$表示。因为两个矢量所在的坐标系具有相同的姿态，通过矢量相加的方法求点$P$相对于$A$的位置${}^{A}P$：

$${}^{A}P={}^{B}P+{}^A{P}_{BORG}\text{\hspace{1em}(2-12)}$$

图2.4 平移坐标变换

2.2.2 旋转变换

如图2.5 所示，坐标系$B$和$A$的坐标原点重合，但两者的方向不同。坐标系相对于坐标系的姿态描述用旋转矩阵表示，空间中的点$P$在坐标系$A$的位置描述为${}^{A}P$，在坐标系$B$的位置描述为${}^{B}P$，两者具有如下变换关系：

$${}^{A}P={}_B^{A}R{}^{B}P\text{\hspace{1em}(2-13)}$$

图2.5 旋转坐标变换

1. 绕一个坐标轴旋转的旋转矩阵

绕 X,Y,Z 坐标轴的旋转变换矩阵是最基本的转动矩阵，他们是一般转动矩阵的特例，故可直接由一般转动矩阵得到。

图2.6 绕 X 轴，Y 轴，Z 轴转动 θ 角

绕 X 轴，Y 轴，Z 轴转动 θ 角对应的旋转矩阵为：

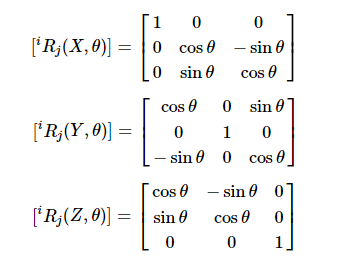
2. 绕多个坐标轴旋转的旋转矩阵

坐标系绕多个坐标轴转动问题可分为绕动坐标系的旋转（内在旋转）和绕定坐标系的旋转（外在旋转）。

1） 绕动坐标系的旋转

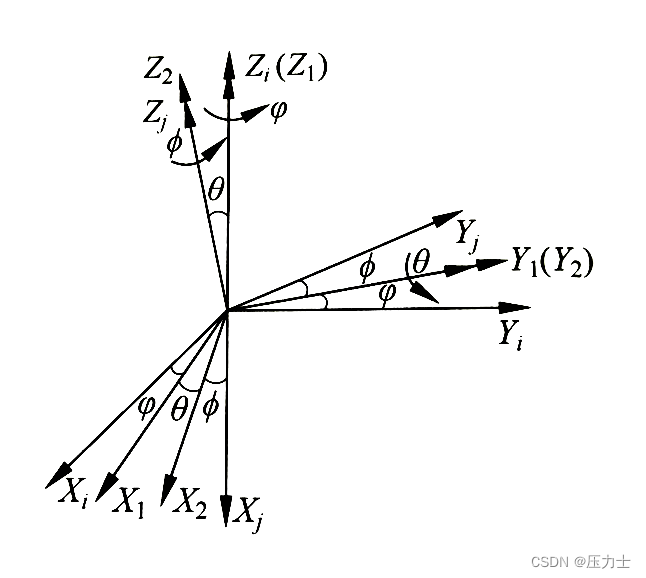
坐标系{i}\{i\}{i}绕其 Z 轴旋转$\phi$角，得到新坐标系 {1}， 坐标系 {1} 再绕其 Y 轴旋转$\theta$角，得到新坐标系 {2}，坐标系 {2} 再绕其 Z 轴旋转$\varphi$角，得到新坐标系{j}\{j\}{j}， 旋转矩阵 ${}_i^{j}R(\phi ,\theta ,\varphi )$：

图 2.7 绕动坐标系的坐标轴旋转示意图
旋转矩阵为：

2） 绕定坐标系的旋转

坐标系{i}\{i\}{i}绕其 X 轴旋转$\alpha$角，得到新坐标系{m}\{m\}{m}， 坐标系{m}\{m\}{m}再绕坐标系{i}\{i\}{i}的 Z 轴旋转$\theta$角，得到新坐标系{j}\{j\}{j}， 旋转矩阵 ${}_i^{j}R(\alpha ,\theta )$：

图 2.8 绕定坐标系旋转示意图

旋转矩阵为：

绕动坐标系旋转，转动矩阵右乘，旋转矩阵相乘顺序与坐标系转动次序相同；绕定坐标系旋转，转动矩阵左乘，旋转矩阵相乘顺序与坐标系转动次序相反；内在旋转与外在旋转的绕轴旋转序列倒序时，两者等效。

2.2.3 复合变换

通常情况下存在这样的情况，假设已知矢量相对某坐标系$B$的描述，但想求其相对于另一个坐标系$A$的描述，此时需要同时用到平移和旋转变换。如图2.9 所示，坐标系$A$和坐标系$B$原点不同且姿态不同，已知空间中的点$P$相对于坐标系$B$的描述为${}^{B}P$，那么相对于坐标系的描述可以通过复合变换得到。首先通过旋转变换，将$P$的姿态变换到一个中间坐标系，该中间坐标系和坐标系$A$的姿态相同，但原点与坐标系$B$重合，然后再将中间坐标系进行平移变换，使其与坐标系$A$重合。其变换的过程见式（2-14）所示。

$${}^{A}P={}_B^{A}R{}^{B}P+{}^A{P}_{BORG}\text{\hspace{1em}(2-14)}$$

图 2.9 复合变换

为了方便计算，一般我们将式(2-14)写成如下表示形式：

$$\left[\begin{array}{c}{}^{A}P\\ \\ 1\end{array}\right]=\left[\begin{array}{cc}{}_B^{A}R& {}^A{P}_{BORG}\\ & \\ \text{0}& 1\end{array}\right]\left[\begin{array}{c}{}^{B}P\\ \\ 1\end{array}\right]\Rightarrow AP={}_B^{A}T{}^{B}P\text{\hspace{1em}(2-15)}$$

其中，${}^{A}P$ 和 ${}^{B}P$ 均为 4×1 的列向量，${}_B^{A}T$ 为 4×4 的齐次变换矩阵，表示坐标系 $B$ 相对于坐标系 $A$ 的变换描述。

2.3 齐次坐标和齐次变换

齐次坐标可用于表征机器人的位姿，齐次变换可用于实现不同坐标系中机器人位姿的转换。

2.3.1 齐次坐标

（1）点的齐次坐标

一般来说，n 维空间的齐次坐标表示是一个 n+1 维空间实体。有一个特定的投影附加于 n 维空间，也可以把它看作一个附加于每个矢量的特定坐标——比例系数。
简而言之，齐次坐标就是用 n+1 维来代表 n 维坐标.

我们可以在一个 3×1 维的笛卡尔坐标末尾加上一个额外的变量 $\omega$ 来形成 4×1 维的齐次坐标。因此，一个在笛卡尔坐标系下的点 $\mathbf{P}=[xyz{]}^T$ 在齐次坐标里面变成了 $\mathbf{P}=[abcw{]}^T$ ，并且有

$x=a/\omega$，$y=b/\omega$，$z=c/\omega$，其中，$\omega$是非零实数。

例如，笛卡尔坐标系下 $\mathbf{P}=[123{]}^T$ 用齐次坐标可以表示为 $\mathbf{P}=[1231{]}^T$

显然，齐次坐标表达并不是唯一的，随$\omega$ 值的不同而不同。在计算机图学中，$\omega$ 作为通用比例因子，它可取任意正值，但在机器人的运动分析中，总是取 $\omega$=1。即点的齐次坐标通式为：

$$\mathbf{P}=[xyz1{]}^T$$

（2）坐标轴的齐次坐标

坐标轴齐次坐标通式：

$[abc0{]}^T$，其中a, b, c 称为方向数

笛卡尔坐标系三个坐标轴的齐次坐标表示如下：

（1）X 轴的齐次坐标为：$[1000{]}^T$;
（2）Y 轴的齐次坐标为：$[0100{]}^T$;
（3）Z 轴的齐次坐标为：$[0010{]}^T$.

2.3.2 齐次变换

坐标系{j}\{j\}{j}相对于坐标系{i}\{i\}{i}的平移向量 ${}_i^{O_j}\mathbf{P}$ 的齐次变换矩阵：

$$\mathbf{Trans}{(}_i^{O_j}\mathbf{P})=\left[\begin{array}{cccc}& {\mathbf{I}}_{3\times 3}& & {}_i^{O_j}\mathbf{P}\\ & & & \\ 0& 0& 0& 1\end{array}\right]$$

坐标系{j}\{j\}{j}相对于坐标系{i}\{i\}{i}的旋转向量 ${}_i^j\mathbf{R}$ 的齐次变换矩阵：

$$\mathbf{Rot}(\mathbf{K},\theta )=\left[\begin{array}{cccc}& {}_i^j\mathbf{R}& & 0\\ & & & \\ 0& 0& 0& 1\end{array}\right]$$

综合齐次变换矩阵：

$${}_i^j\mathbf{T}={\left[\begin{array}{cccc}& {}_i^j\mathbf{R}& & {}_i^{O_j}\mathbf{P}\\ & & & \\ 0& 0& 0& 1\end{array}\right]}_{4\times 4}$$

${}_i^j\mathbf{T}$ 的含义是坐标系{j}\{j\}{j}相对于坐标系{i}\{i\}{i}的位姿。

2.4 姿态的其他表示方法

2.4.1 RPY角

绕固定坐标系多个坐标轴旋转，定义绕 Z 轴的转动为 Roll（翻滚），转角为 α； 绕 Y 轴的转动为 Pitch（俯仰），转角为 β；绕 X 轴的转动为 Yaw（偏航），转角为 γ 。

顺序：绕 X 转 γ，绕 Y 转 β，绕 Z 转 α，旋转矩阵左乘。

公式：$R_{xyz}(\gamma ,\beta ,\alpha )=Rot(Z,\alpha )Rot(Y,\beta )Rot(X,\gamma )$

2.4.2 欧拉角

ZYX欧拉角

绕自身坐标系，绕动轴 Z—Y—X 旋转，旋转矩阵右乘。

顺序：绕 Z 转 α，绕 Y 转 β，绕 X 转 γ 。

公式：$R_{zyx}(\alpha ,\beta ,\gamma )=Rot(Z,\alpha )Rot(Y,\beta )Rot(X,\gamma )$

ZYZ欧拉角

只需要两个坐标轴，绕动轴 Z—Y—Z 旋转，旋转矩阵右乘。

顺序：绕 Z 转 α，绕 Y 转 β，绕 Z 转 γ 。

公式：$R_{zyz}(\alpha ,\beta ,\gamma )=Rot(Z,\alpha )Rot(Y,\beta )Rot(Z,\gamma )$