#!/usr/bin/python
# -*- coding: utf-8 -*-
import math
import random
import operator

'''
zys 2016-10-01
本程序实现的是C4.5(包含ID3的实现)
参考： http://blog.csdn.net/lulei1217/article/details/49583357
过程:
1、创建决策树
    1)通过计算增量熵查找第一个最优特征分类
    2)根据分类的特征如(0,1)分别去除掉数据中已经确定的分类数据
    3)通过计算新数据增量熵查找下一个最优特征
    4)返回导第二步骤，直到符合循环终止条件
        条件一：其当前分类特征全部相同
        条件二：所有特征都已经分类
2、进行悲观剪枝
3、使用决策树进行测试分类
'''


def createTree(traindata, labels):
    '''创建决策树'''
    classList = [item[-1] for item in traindata]
    '''
    当前特征分类的labels全部相同的时候停止分类，直接返回任意一个label
    例如：当badrecord(不良记录) = 1时候,offer全部都为0 这时候直接返回0
    '''
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(traindata[0]) == 1:
        return majorityCnt(classList)
    bestFeature = chooseBestFeature(traindata)  # 获取最优分类特征
    bestFeatLabel = labels[bestFeature]
    tree = {bestFeatLabel: {}}
    featureList = [example[bestFeature] for example in traindata]
    uniqueVals = set(featureList)
    ''''
    循环对后续特征分类
    去除掉已经选择的特征和数据
    '''
    del(labels[bestFeature])
    for feature in uniqueVals:
        A = getLablesByfeature(traindata, bestFeature, feature)
        tree[bestFeatLabel][feature] = createTree(A, labels[:])
    return tree


def majorityCnt(classList):
    '''当对最后一个特征进行分类时候，直接返回当前出现最多的labels'''
    classCount = {}
    for vote in classList:
        classCount[vote] = classCount.get(vote, 0) + 1
    # key=operator.itemgetter(1) 定义函数key，获取对象的第1个域的值
    sortedClassCount = sorted(classCount.items(),
                              key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]


def chooseBestFeature(traindata):
    '''
    选择最优特征
    在ID3中获取信息熵的增益：Gain(S,A) = Entropy(S) - ∑(|A| / |S|) * Entropy(A)
    在C4.5中获取的是信息熵的增益率：
    SplitInfo(A) = - ∑(|A| / |S|) * log2(|A| / |S|)
    GainRate(S,A) = Gain(S,A) / SplitInfo(A)
    Entropy(S) 指总集合S的信息信息熵
    A 是S中的某个属性的子集
    |S| 指集合S的样例数data
    '''
    size = len(traindata[0]) - 1   # 获取特征的数量
    Entropy = calculateEntropy(traindata)  # 计算总集合的信息熵 Entropy(S)
    GainRate = 0.0
    bestFeature = -1
    for i in range(size):
        '''
        获取当前特征的子集,例如：
        school 对应着[0,0,0,0,1,1,1,1]
        '''
        featureList = [example[i] for example in traindata]
        '''
        获取当前特征的分类,例如
        school 对应着[0,1] 名校、不是名校
        '''
        uniqueVals = set(featureList)
        newEntropy = 0.0
        splitInfo = 0.0
        for feature in uniqueVals:
            A = getLablesByfeature(traindata, i, feature)
            prob = float(len(A)) / len(traindata)
            # 计算特征子集的信息熵 Entropy(A)
            newEntropy += prob * calculateEntropy(A)
            info = 0.0
            if(prob != 0):
                info = math.log(prob, 2)
            splitInfo -= prob * info
        newGain = Entropy - newEntropy  # 计算信息增益
        if (splitInfo == 0):  # 修复溢出错误
            splitinfo = -0.99 * math.log(0.99, 2) - 0.01 * math.log(0.01, 2)
        newGain = newGain / splitInfo
        if (newGain > GainRate):
            GainRate = newGain
            bestFeature = i
    return bestFeature

'''
ID3 中的代码：
def chooseBestFeature(traindata):
    size = len(traindata[0]) - 1
    Entropy = calculateEntropy(traindata)
    Gain = 0.0
    bestFeature = -1
    for i in range(size):
        uniqueVals = set(featureList)
        newEntropy = 0.0
        for feature in uniqueVals:
            A = getLablesByfeature(traindata, i, feature)
            prob = float(len(A)) / len(traindata)
            newEntropy += prob * calculateEntropy(A)
        newGain = Entropy - newEntropy
        if (newGain > Gain):
            Gain = newGain
            bestFeature = i
    return bestFeature
'''


def getLablesByfeature(traindata, index, feature):
    '''
    通过特征来获取对应的Lables，例如：
    获取school=0,多对应的Lables [0,0,1,0]
    '''
    A = []
    for item in traindata:
        if item[index] == feature:
            temp = item[:index]  # 抽取除index特征外的所有的记录的内容
            temp.extend(item[index + 1:])
            A.append(temp)
    return A


def calculateEntropy(data):
    '''
    计算信息熵 Entropy=-∑P(ui)*log(P(ui))
    P(ui)是类别ui出现概率
    '''
    labelCount = {}
    for item in data:
        lable = item[-1]
        labelCount[lable] = labelCount.get(lable, 0) + 1
    entropy = 0.0
    for key in labelCount:
        p = float(labelCount[key]) / len(data)
        entropy -= p * math.log(p, 2)
    return entropy


def classify(tree, lables, item):
    '''
    测试
    tree.keys()找出所有的key，在获取对应的key值时候需要将其改变为list类型
    '''
    root = list(tree.keys())[0]
    nextNode = tree[root]
    index = lables.index(root)
    key = item[index]
    val = nextNode[key]
    '''
    判断valueOfFeat是否是dict类型
    如果是说明其还有子节
    不是则表示没有子节点，返回的值就是其对应的分类
    '''
    if(isinstance(val, dict)):
        classLabel = classify(val, lables, item)
    else:
        classLabel = val
    return classLabel


def getCount(tree, data, lables, count):
    root = list(tree.keys())[0]
    nextNode = tree[root]
    index = lables.index(root)
    del(lables[index])
    for key in nextNode.keys():
        rightcount = 0
        wrongcount = 0
        A = getLablesByfeature(data, index, key)
        # 判断是否是叶子节点，不是则迭代进入下一层
        if(isinstance(nextNode[key], dict)):
            getCount(nextNode[key], A, lables[:], count)
        else:
            for item in A:
                # 判断数组给定的分类是否与叶子节点的值相同
                if(str(item[-1]) == str(nextNode[key])):
                    rightcount += 1
                else:
                    wrongcount += 1
            count.append([rightcount, wrongcount])


def cutBranch(tree, data, lables):
    '''
    悲观剪枝 参考：http://www.jianshu.com/p/794d08199e5e
    old = errorNum + o.5 * L  errorNum:叶子节点错误分类的个数，L：叶子节点个数
    p = old / N  N:数据样本总个数
    new = errorNum + o.5
    S = math.sqrt(N  * p * (1 - p))
    if new <= old - S then 剪枝

    注：都是自己理解的，如果有不对的地方欢迎指出
    '''
    root = list(tree.keys())[0]
    nextNode = tree[root]
    index = lables.index(root)
    newTree = {root: {}}
    del(lables[index])
    for key in nextNode.keys():
        # 如果子节点不是叶子节点就判断其是否满足剪枝
        if(isinstance(nextNode[key], dict)):
            A = getLablesByfeature(data, index, key)
            count = []
            # 获取每个叶子节点的(正确分类数，错误分类数)
            getCount(nextNode[key], A, lables[:], count)
            allnum = 0
            errornum = 0
            for i in count:
                allnum += i[0] + i[1]
                errornum += i[1]
            if(errornum == 0):
                # 当该子树不存在错误分类的时候，不对该树进行剪枝操作
                # 进行下个循环
                newTree[root][key] = nextNode[key]
                continue
            old = errornum + len(count) * 0.5
            new = errornum + 0.5
            p = old / allnum
            S = math.sqrt(allnum * p * (1 - p))
            if(new <= old - S):
                # 用当前分类时出现最多的lables代替该子树
                classList = [item[-1] for item in A]
                newTree[root][key] = majorityCnt(classList)
            else:
                # 不满足剪枝则进入其子树内部继续进行剪枝操作
                newTree[root][key] = cutBranch(nextNode[key], A, lables[:])
        else:
            newTree[root][key] = nextNode[key]
    return newTree

if(__name__ == "__main__"):
    '''
    -----------------------------开始-----------------------------
    公司校园招聘
    名校    技术能力    不良记录    是否录取
    是(1)   厉害(1)     有(1)      录取(1)
    否(0)   一般(0)     无(0)      不录取(0)

    data = [[0, 0, 0, 0],
            [0, 0, 1, 0],
            [0, 1, 0, 1],
            [0, 1, 1, 0],
            [1, 0, 0, 1],
            [1, 0, 1, 0],
            [1, 1, 0, 1],
            [1, 1, 1, 0]]
    lables = ["school", "ability", "badrecord", "offer"]
    '''
    # data = [['youth', 'high', 'no', 'fair', 'no'],
    #         ['youth', 'high', 'no', 'excellent', 'no'],
    #         ['middle_aged', 'high', 'no', 'fair', 'yes'],
    #         ['senior', 'medium', 'no', 'fair', 'yes'],
    #         ['senior', 'low', 'yes', 'fair', 'yes'],
    #         ['senior', 'low', 'yes', 'excellent', 'no'],
    #         ['middle_aged', 'low', 'yes', 'excellent', 'yes'],
    #         ['youth', 'medium', 'no', 'fair', 'no'],
    #         ['youth', 'low', 'yes', 'fair', 'yes'],
    #         ['senior', 'medium', 'yes', 'fair', 'yes'],
    #         ['youth', 'medium', 'yes', 'excellent', 'yes'],
    #         ['middle_aged', 'medium', 'no', 'excellent', 'yes'],
    #         ['middle_aged', 'high', 'yes', 'fair', 'yes'],
    #         ['senior', 'medium', 'no', 'excellent', 'no']]
    # lables = ['age', 'income', 'student', 'credit_rating']
    data = [['dark_green', 'curl_up', 'little_heavily', 'distinct', 'sinking', 'hard_smooth', 1],
            ['black', 'curl_up', 'heavily', 'distinct', 'sinking', 'hard_smooth', 1],
            ['black', 'curl_up', 'little_heavily',
                'distinct', 'sinking', 'hard_smooth', 1],
            ['dark_green', 'little_curl_up', 'little_heavily',
             'distinct', 'little_sinking', 'soft_stick', 1],
            ['black', 'little_curl_up', 'little_heavily',
             'little_blur', 'little_sinking', 'soft_stick', 1],
            ['dark_green', 'stiff', 'clear', 'distinct', 'even', 'soft_stick', 0],
            ['light_white', 'little_curl_up', 'heavily',
             'little_blur', 'sinking', 'hard_smooth', 0],
            ['black', 'little_curl_up', 'little_heavily',
             'distinct', 'little_sinking', 'soft_stick', 0],
            ['light_white', 'curl_up', 'little_heavily',
             'blur', 'even', 'hard_smooth', 0],
            ['dark_green', 'curl_up', 'heavily', 'little_blur',
             'little_sinking', 'hard_smooth', 0],
            ['dark_green', 'curl_up', 'heavily',
             'distinct', 'sinking', 'hard_smooth', 1],
            ['light_white', 'curl_up', 'little_heavily',
             'distinct', 'sinking', 'hard_smooth', 1],
            ['black', 'little_curl_up', 'little_heavily',
             'distinct', 'little_sinking', 'hard_smooth', 1],
            ['black', 'little_curl_up', 'heavily', 'little_blur',
             'little_sinking', 'hard_smooth', 0],
            ['light_white', 'stiff', 'clear', 'blur', 'even', 'hard_smooth', 0],
            ['light_white', 'curl_up', 'little_heavily',
             'blur', 'even', 'soft_stick', 0],
            ['dark_green', 'little_curl_up', 'little_heavily', 'little_blur', 'sinking', 'hard_smooth', 0]]
    lables = ['color', 'root', 'knocks', 'texture', 'navel', 'touch']

    '''
    传入的是data和lables的复制，因为在函数中会改变该值。
    而python传参传递的是一个地址，因此会改变原本的数据
    '''
    decisiontree = createTree(data[:], lables[:])
    createPlot(decisiontree)
    decisiontree = cutBranch(decisiontree, data, lables[:])
    k = 0
    for item in data:
        if(classify(decisiontree, lables[:], item) == item[-1]):
            k += 1
    print(float(k) / len(data))
    createPlot(decisiontree)

使用matplotlib画出决策树

import matplotlib.pyplot as plt

'''
使用matplotlib的annotate画出决策树
参考： http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.annotate
matplotlib.pyplot.annotate(text,xy,xytext,xycoords,textcoords,arrowprops)
text:注解的内容
xy:箭头指向的坐标
xytext:注解内容的坐标，如果没有默认xy
xycoords:给定xy一个坐标系统
textcoords:给定xytext一个坐标系统
arrowprops:箭头的格式
'''
decisionNode = dict(boxstyle="round4", color='#3366FF')  # 定义判断结点形态
leafNode = dict(boxstyle="circle", color='#FF6633')  # 定义叶结点形态
arrow_args = dict(arrowstyle="<-", color='g')  # 定义箭头


# 绘制带箭头的注释
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


# 计算叶结点数
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


# 计算树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


# 在父子结点间填充文本信息相同
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center",
                        ha="center", rotation=30)


def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) /
              2.0 / plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)  # 在父子结点间填充文本信息
    plotNode(firstStr, cntrPt, parentPt, decisionNode)  # 绘制带箭头的注释
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff,
                                       plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
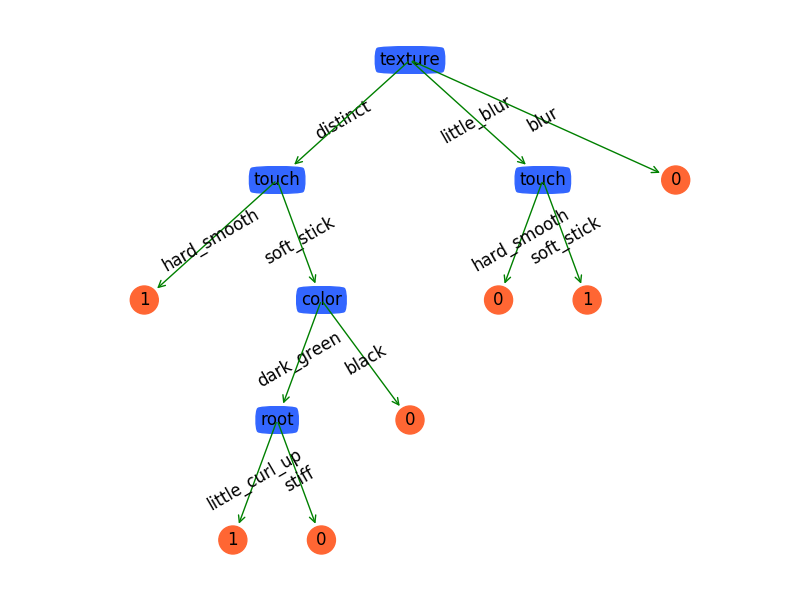
    plt.show()

效果图