神经网络ANN
人工神经网络又称神经网络。神经网络是一种学习器,给他一组输入,他会得到一组输出,神经网络里的结点相互连接决定了输入的数据在里面经过怎样的计算。我们可以通过大量的输入,让神经网络调整它自身的连接情况从而总是能够得到我们预期的输出。神经网络对于逼近实数值、离散值或向量值的目标函数提供了一种健壮性很强的方法,现在已经成功应用到很多领域,例如视觉场景分析,手写字符识别,语音识别、人脸识别等。需要学习的目标
人工神经网络又称神经网络。神经网络是一种学习器,给他一组输入,他会得到一组输出,神经网络里的结点相互连接决定了输入的数据在里面经过怎样的计算。我们可以通过大量的输入,让神经网络调整它自身的连接情况从而总是能够得到我们预期的输出。
神经网络对于逼近实数值、离散值或向量值的目标函数提供了一种健壮性很强的方法,现在已经成功应用到很多领域,例如视觉场景分析,手写字符识别,语音识别、人脸识别等。需要学习的目标函数是定义在可以用向量描述的实例上,向量由预先定义的特征组成,比如字符识别,那么特征可以是图像中的每个像素亮度值。
单层神经网络-多层神经网络-深度学习(卷积神经网络)
- 感知器的概念
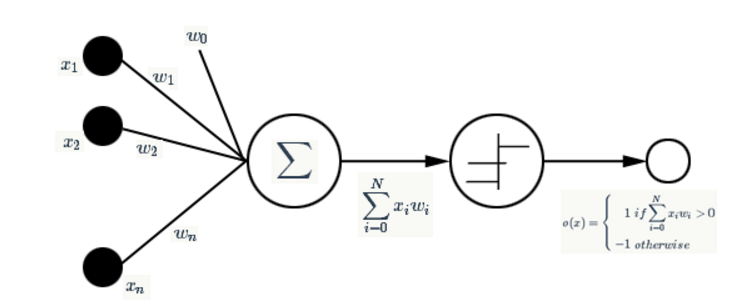
感知器实际上是神经网络结构中的一个神经元,那么一个感知器就够成了最简单的神经网络系统(虽然还算不上是网络)。感知器是以一组实数向量作为输入,计算这些输入的线性组合,如果结果大于某个阈值就输出1,否则就输出-1。
我们可以把感知器看成n维实例空间(点空间)中的超平面的决策面,平面一侧的所有实例输出为1,对另一侧的实例输出-1。这个决策超平面的方程是 ω→⋅x→=0 <script type="math/tex" id="MathJax-Element-423">\overrightarrow{\omega}\cdot\overrightarrow{x}=0</script>。
这个含义对应了样本数据的2分类问题,其中一种样本,感知器总是输出1,而另一类总是输出-1。但是显然这个决策超平面只能对于线性可分的空间才能存在。
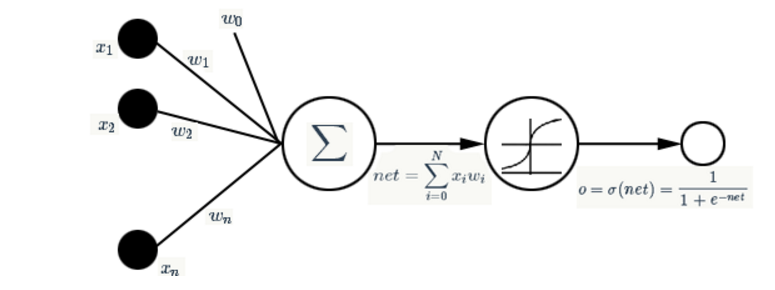
我们希望找到一组这样的权值,对于我们输入的每一组向量,总能够得到一个我们期望的值。在实际的模式分类的应用中,样本空间往往并不是线性的。我们要找到一种非线性映射,于是激活函数产生了。激活函数是一种非线性函数同时是可微函数,对于可微,因为我们需要知道权重是怎样影响最终输出的,我们要根据输出来调节那些权重向量。也就是使用了梯度下降法则。
常用的激活函数就是S型激活函数 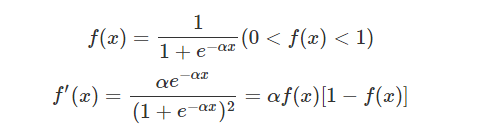
经过这样的非线性映射,我们的感知器(现在应该叫SIMGOID单元)就变成了下面这种结构:
对于很多组这样的输入样本,我们可以通过不断的调整权值,来让他们的输出接近于我们预想的输出。
- 反向传播算法
为了找到最合适的权值向量,需要一定的规则指导我们的搜索,梯度下降方法就是这样的方法,首先我们定义输出误差,即对于任意一组权值向量得到的输出与预想的输出之间的误差值。
总的误差使用下式衡量:
我们就是要找到一组权值让这个误差的值最小。神经网络大多采取正向传播预测,反向传播误差的结构。反向传播算法是运用在神经网络中进行网络权重等最优值计算算法,其核心是梯度下降和链式法则求偏导。
关于 反向传播的推导公式:大家可以参考 http://blog.csdn.net/qrlhl/article/details/50885527
每一层所产生的误差会逐渐向之前的层次传播,而各层的权重根据梯度下降算法不断地优化。总之,反向传播算法的核心就是梯度下降 + 链式法则求偏导,虽然看起来很繁琐并且计算复杂度有点高,但是实际上BP算法的精确性和易用性是很难被其他算法替代的,这也是现在比如CNN等很火的深度学习算法普遍采用BP算法的原因。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容
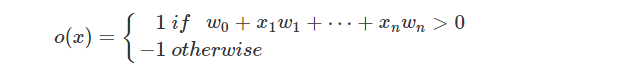
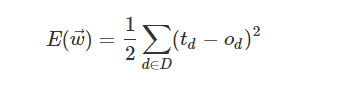








所有评论(0)