关联度分析

关联度分析是指给出物品或对象的相似度。主要有以下的应用场景。

1. 给目标受众提供不同的服务或者广告
2. 电影推荐或者淘宝商品推荐
3. 基因分析，发现共同的祖先

物品推荐

为了简化代码，我们只同时考虑两个物品。比如用户A买了牛奶和面包。我们希望遵循一个原则：如果用户A买了X，那么他很有可能也买Y。

加载数据集

import numpy as np
file = "affinity_dataset.txt"
X = np.loadtxt(file)
n_samples,n_features = X.shape
print("This dataset has {0} samples and {1} features".format(n_samples,n_features))
# the name of your features
features=["bread","milk","cheese","apples","bananas"]

使用排序规则

我们希望根据上面的简单规则：**如果用户A买了X，那么他很有可能也买Y。**去选择合适的规则来给用户进行推荐。而规则的选择主要根据支持度和置信度来判断。

• Support（支持度）：表示同时包含A和B的事务占所有事务的比例。如果用P(A)表示使用A事务的比例，那么Support=P(A&B)
• Confidence（可信度）：表示使用包含A的事务中同时包含B事务的比例，即同时包含A和B的事务占包含A事务的比例。公式表达：Confidence=P(A&B)/P(A)
• Support表示规则发生频率，而Confidence表示规则使用的准确度。

# how many rows contain our premise(前提: that a person is buying apples
num_apples_purchases = 0
for sample in X:
    if sample[3] == 1:
        num_apples_purchases += 1
print("{0} people bought apples".format(num_apples_purchases)
# 36 people bought apples

# how many of the cases that a person bought an apple involved with bananas?
# record both cases where the rule is valid or invalid
valid_rules = 0
invalid_rules = 0
for sample in X:
    if sample[3] == 1:
        if sample[4] == 1:
            valid_rules += 1
        else:
            invalid_rules += 1
print("{0} cases of valid rules were discovered".format(valid_rules))
print("{0} cases of invalid rules were discovered".format(invalid_rules))
# 21 cases of valid rules were discovered
# 15 cases of invalid rules were discovered

#compute the support and confidence 
support = valid_rules
confidence = support / num_apples_purchases
print("The support is {0} and the confidence is {1:.3f}".format(support,confidence))
print("As a percentage, the confidence is {0:.1f}%".format(confidence*100))
# The support is 21 and the confidence is 0.583
# As a percentage, the confidence is 58.3%

计算所有规则的Support 和 Confidence

from collections import defaultdict
valid_rules = defaultdict(int)
invalid_rules = defaultdict(int)
num_occurances = defaultdict(int)

#iterate over each sample and feature
for sample in X:
    for premise in range(n_features):
        # 如果前提条件不存在,比如如果我们买了苹果
        if sample[premise] == 0:
            continue
        num_occurances[premise] += 1
        # 结论,同时我们买了牛奶
        for conclusion in range(n_features):
            # 如果买了苹果，同时买了苹果
            if premise == conclusion:
                continue
            if sample[conclusion] == 1:
                valid_rules[(premise,conclusion)] += 1
            else:
                invalid_rules[(premise,conclusion)] += 1

support = valid_rules
confidence = defaultdict(float)
for premise,conclusion in valid_rules.keys():
    rule = (premise,conclusion)
    confidence[rule] = valid_rules[rule] / num_occurances[premise]

for premise, conclusion in confidence:
    premise_name = features[premise]
    conclusion_name = features[conclusion]
    print("Rule: If a person buys {0} they will also buy {1}".format(premise_name, conclusion_name))
    print(" - Confidence: {0:.3f}".format(confidence[(premise, conclusion)]))
    print(" - Support: {0}".format(support[(premise, conclusion)]))
    print("")

排序发现最好的规则

# rank the best rule
# because of the dict do not support by odering,the items() give us a list
# using itemgetter(1) which allows the sorting based on the values 
from operator import itemgetter
sort_support = sorted(support.items(),key = itemgetter(1),reverse=True)
print(sort_support)

# print the top five rules
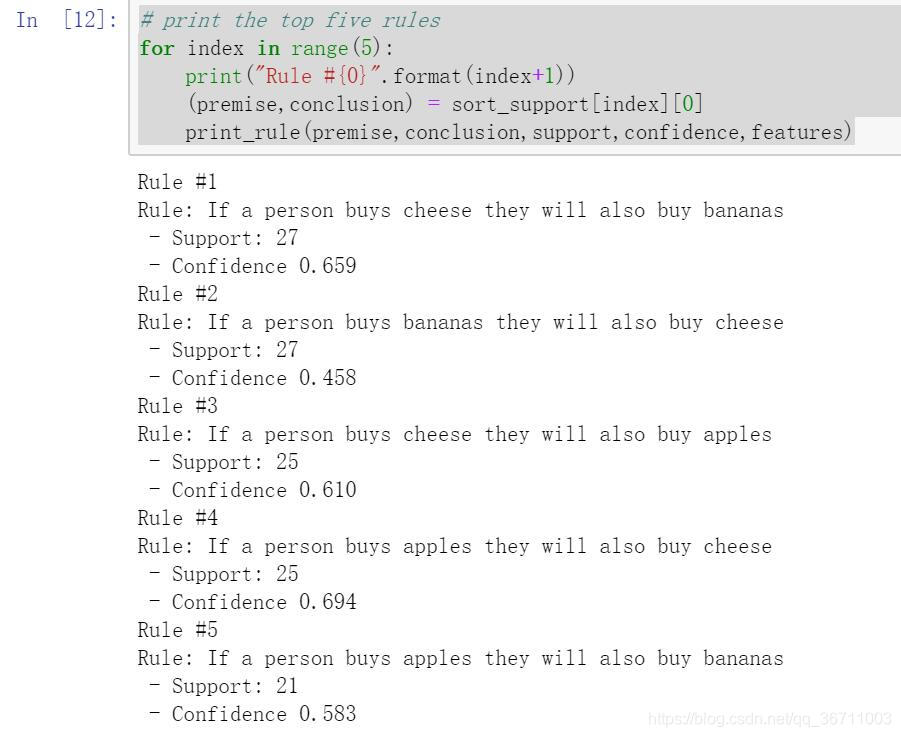
for index in range(5):
    print("Rule #{0}".format(index+1))
    (premise,conclusion) = sort_support[index][0]
    print_rule(premise,conclusion,support,confidence,features)

# based on the confidence
print(confidence.items())
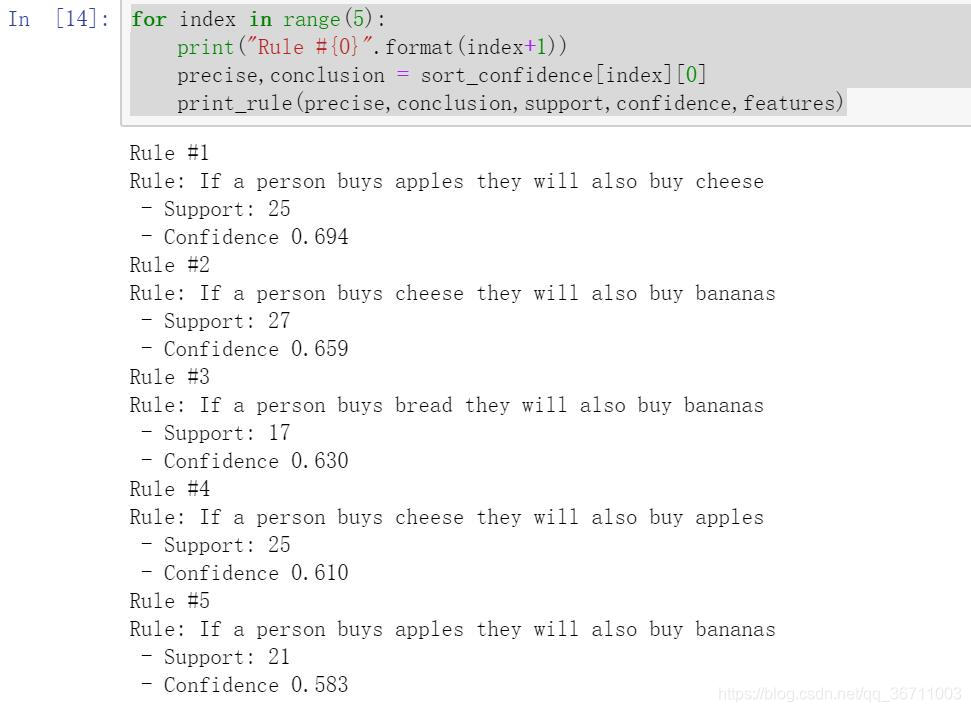
sort_confidence = sorted(confidence.items(),key = itemgetter(1),reverse = True)
for index in range(5):
    print("Rule #{0}".format(index+1))
    precise,conclusion = sort_confidence[index][0]
    print_rule(precise,conclusion,support,confidence,features)

结果展示

鸢尾花分类

分类问题主要有以下应用场景：

1. 判定植物种类
2. 判定图片是不是为狗
3. 判定病人是不是患了癌症根据已有的测试数据…

加载数据集

import numpy as np
from sklearn.datasets import load_iris
dataset = load_iris()
X = dataset.data
y = dataset.target
print(dataset.DESCR)
n_samples,n_features = X.shape

# comnpute the mean for each feature
feature_mean = X.mean(axis = 0)
# 断言语句
assert feature_mean.shape == (n_features,)
X_d = np.array(X >= feature_mean,dtype='int')
print(X_d)

# split the dataset to the train_data and test_data
from sklearn.cross_validation import train_test_split

random_state = 14

X_train,X_test,y_train,y_test = train_test_split(X_d,y,random_state = random_state)
print("There are {0} training samples".format(y_train.shape))
print("There are {0} test samples".format(y_test.shape))

使用OneR算法

OneR的思路很简单，建立一个只针对于单个属性进行测试的规则，并进行不同的分支。每个分支对应的不同属性值。

分支的类就是原始数据（训练数据）在这个分支上出现最多的类。

每一个属性都会产生一个不同的规则集，每条规则对应这个属性的每个值。对每个属性值的规则集的误差率进行评估，选择效果最好的一个即可。

伪代码表述：

对于这个属性的每个属性值，建立如下规则

1. 计算每个类别出现的频率
2. 找出出现最频繁的类别找出出现最频繁的类别
3. 建立规则，将这个类别赋予这个属性值建立规则，将这个类别赋予这个属性值
4. 计算规则的误差率计算规则的误差率
5. 选择误差率最小的规则选择误差率最小的规则

比如，如果特征X有两个值0，1。对于0，我们发现有20个是属于A，60个属于B，20个属于C。那么对于X = 0的预测是属于A，有40/100 = 0.4的误差。

from collections import defaultdict
from operator import itemgetter

# use the oneR algorithm
#训练特征的值
def train_feature_value(X,y_true,feature,value):
    # count the actual classes for each sample with that feature value
    class_counts = defaultdict(int)
    for sample,y in zip(X,y_true):
        if sample[feature] == value:
            class_counts[y] += 1
    # find the most frequently assigned class by sorting the class_counts
    sort_class_counts = sorted(class_counts.items(),key=itemgetter(1),reverse = True)
    most_frequent_class = sort_class_counts[0][0]
    # compute the error
    # The error is the number of samples that do not classify as the most frequent class
    incorrect_predictions = [class_count for class_value,class_count in class_counts.items() if class_value != most_frequent_class]
    error = sum(incorrect_predictions)
    
    return most_frequent_class,error

def train(X,y_true,feature):
    """Computes the predictors and error for a given feature using the OneR algorithm
    
    Parameters
    ----------
    X: array [n_samples, n_features]
        The two dimensional array that holds the dataset. Each row is a sample, each column
        is a feature.
    
    y_true: array [n_samples,]
        The one dimensional array that holds the class values. Corresponds to X, such that
        y_true[i] is the class value for sample X[i].
    
    feature: int
        An integer corresponding to the index of the variable we wish to test.
        0 <= variable < n_features
        
    Returns
    -------
    predictors: dictionary of tuples: (value, prediction)
        For each item in the array, if the variable has a given value, make the given prediction.
    
    error: float
        The ratio of training data that this rule incorrectly predicts.
    """
    
    # Check that variable is a valid number
    n_samples, n_features = X.shape
    assert 0 <= feature < n_features
    # Get all of the unique values that this variable has
    values = set(X[:,feature])
    # Stores the predictors array that is returned
    predictors = dict()
    # store the errors for each feature value
    errors = []
    
    # iterate over all the unique feature values to find most_frequent_class and error
    for cur_value in values:
        most_frequent_class,error = train_feature_value(X,y_true,feature,cur_value)
        predictors[cur_value] = most_frequent_class
        errors.append(error)
    total_error = sum(errors)
    return predictors,total_error

# compute all the predictors and errors for the features
all_predictors = {}
errors = {}
for feature in range(X_train.shape[1]):
    predictors,total_error = train(X_train,y_train,feature)
    all_predictors[feature] = predictors
    errors[feature] = total_error
# find the best feature with the lowest error
best_feature,best_error = sorted(errors.items(),key=itemgetter(1))[0]
print("The best model  based on the feature {0} and its error {1:.2f}".format(best_feature,best_error))

模型结果

# create our model bt storing the predictors for the best feature
# The model is a dict thate  tells us which feature to use for One Rule and the predictions that are made based on the value it has.
model = {'feature':best_feature,'predictor':all_predictors[best_feature]}
print(model)

# 预测测试集
def predict(X_test,model):
    feature = model['feature']
    predictor = model['predictor']
    y_predicted = np.array([predictor[int(sample[feature])] for sample in X_test])
    return y_predicted

y_predicted = predict(X_test,model)
print(y_predicted)

# compute the accuracy
accuracy = np.mean(y_predicted == y_test)*100
print("The test accuracy is {0:.1f}%".format(accuracy))

由于模型构造比较简单，所以准确率也就只有65.8%。