线性判别分析LDA(Linear Discriminant Analysis)又称为Fisher线性判别，是一种监督学习的降维技术，也就是说它的数据集的每个样本都是有类别输出的，这点与PCA（无监督学习）不同。LDA在模式识别领域（比如人脸识别，舰艇识别等图形图像识别领域）中有非常广泛的应用，因此我们有必要了解下它的算法原理。

1. LDA的思想

LDA的思想是：最大化类间均值，最小化类内方差。意思就是将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远。

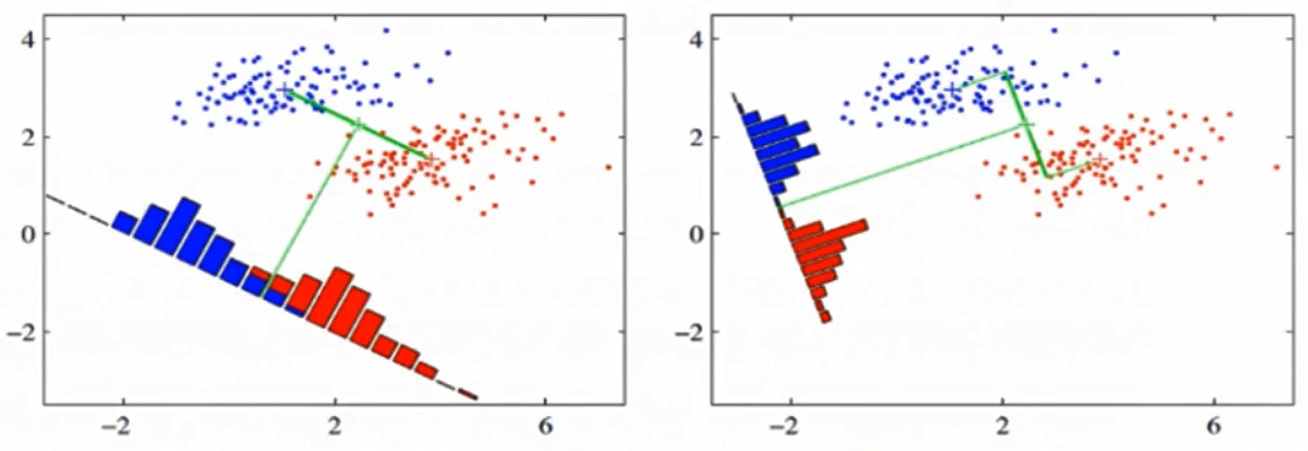
我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

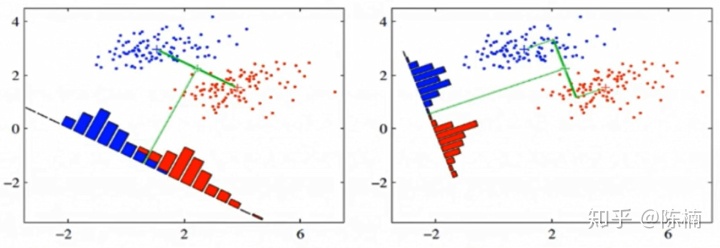
上图提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

2. 瑞利商(Rayleigh quotient)与广义瑞利商(genralized Rayleigh quotient)

首先来看瑞利商的定义。瑞利商是指这样的函数

其中，

共轭转置矩阵和自己相等的矩阵，即

瑞利商

它的最大值等于矩阵 A 最大的特征值，而最小值等于矩阵 A 的最小的特征值，也就是满足

当向量

下面看一下广义瑞利商。广义瑞利商是指这样的函数

其中

而分子转化为：

此时我们的

利用前面的瑞利商的性质，我们可以很快的知道，

2. LDA的原理及推导过程

假设样本共有

设

此处设

假设第K类样本的数据集为

第

各个类别的样本方差之和：

其中，

不同类别

所有类别之间的距离之和为：

其中，

在已知条件下，

“类间距离尽可能大，类内方差尽可能小”，即最大化

令

为了使所求最大，可假设

证明

为对称矩阵：

所以，

为对称矩阵，同理可证明

为对称矩阵。

计算矩阵

注意: (1)选取特征值时，如果一些特征值明显大于其他的特征值，则取这些取值较大的特征值，因为它们包含更多的数据分布的信息。相反，如果一些特征值接近于0，我们将这些特征值舍去。
(2)由于 W 是一个利用了样本类别得到的投影矩阵，因此它能够降维到的维度d的最大值为 K-1 。为什么不是 K 呢？因为

中每个

的秩均为1(因为

为1维向量).

由

知，

又

对应的特征向量至少有

个，也就是说 d 最大为

.

3. LDA算法流程

输入：数据集

输出：降维后的数据集

1）计算类内散度矩阵

2）计算类间散度矩阵

3）计算矩阵

4）计算矩阵

5）对样本集中的每一个样本特征

6）得到输出样本集

4. LDA与PCA对比

LDA与PCA都可用于降维，因此有很多相同的地方，也有很多不同的地方

相同点：

• 两者均可用于数据降维
• 两者在降维时均使用了矩阵特征分解的思想
• 两者都假设数据符合高斯分布

不同点：

• LDA是有监督的降维方法，而PCA是无监督降维方法
• 当总共有K个类别时，LDA最多降到K-1维，而PCA没有这个限制
• LDA除了用于降维，还可以用于分类
• LCA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优（如下图的左图）。当然，某些数据分布下PCA比LDA降维较优（如下图的右图）。

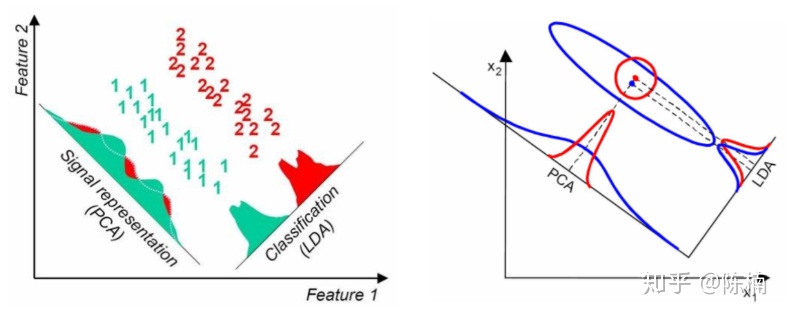
5. LDA算法小结

LDA算法既可以用来降维，也可以用来分来，但是目前来说，LDA主要用于降维，在进行与图像识别相关的数据分析时，LDA是一个有力的工具。下面总结一下LDA算法的优缺点。

LDA算法的优点

• 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习无法使用先验知识；
• LDA在样本分类信息依赖均值而不是方差的时候，比PCA算法较优。

LDA算法的缺点

• LDA与PCA均不适合对非高斯分布样本进行降维
• LDA降维算法最多降到类别数K-1的维度，当降维的维度大于K-1时，则不能使用LDA。当然目前有一些改进的LDA算法可以绕过这个问题
• LDA在样本分类信息依赖方差而非均值的时候，降维效果不好
• LDA可能过度拟合数据

参考：线性判别分析LDA原理总结 - 刘建平Pinard - 博客园