提示：本文上接 机器人运动学笔记1——林沛群

---

前言

本文将涉及到机器人学的正、逆运动学和D-H表达法相关内容。这些内容均来自学习过程中记录的笔记。笔记摘自台大机器人学之运动学——林沛群

---

一、正向运动学

1.1 正向运动学

运动学：讨论运动状态本身(位置姿态速度角速度加速度角加速度时间)，不涉及力。
找出杆件的相对几何状态，在各杆件上建立参考系

1.2 手臂几何描述

• Joint：

   每个转动副会对应一个特定旋转轴和一个DOF。
  

• Link：

   连接两个转动副的杆件，为刚体。
  

• 杆件的编号：

   Link 0：地杆，固定不动的杆件
   Link 1：和link 0相连的杆件
   Link 2：依此类推
  

• 每两个杆件之间需要四个参数表达：

   两个转轴之间的距离link length
   两个转轴之间关于中间垂线相差多少角度link twist
   两杆件转轴偏差link offset 
   转轴转角joint angle		
  

Link length用$a_{i-1}$表示，Link twist 用${\alpha }_{i-1}$表示，Link offset 用$d_i$表示，Joint angle用 ${\theta }_i$表示。对于转动副${\theta }_i$为变量，对于移动副$d_i$为变量。

1.3 D-H表示法

• 建立两动杆刚体坐标系：
  ${\hat{Z}}_i$转动副或者移动副axis方向
  ${\hat{X}}_i$沿着$a_i$方向(if $a_i\ne 0$)，当$a_i=0$时，${\hat{X}}_i$的方向是${\hat{Z}}_i$和${\hat{Z}}_{i+1}$两者垂直
  ${\hat{Y}}_i$与${\hat{X}}_i$和${\hat{Z}}_i$两者垂直，遵守右手定则
  
  

• 建立地杆link 0刚体坐标系：
  一般选取地杆和第一杆件坐标系重合$a_0=0$，${\alpha }_0=0$
  转动副时，坐标系建立在${\theta }_1$为变量，$d_1=0$时的位置，${\theta }_1=0$为初始位置
  移动副时，坐标系建立在$d_1$为变量，${\theta }_1=0$时的位置，$d_1=0$为初始位置
  

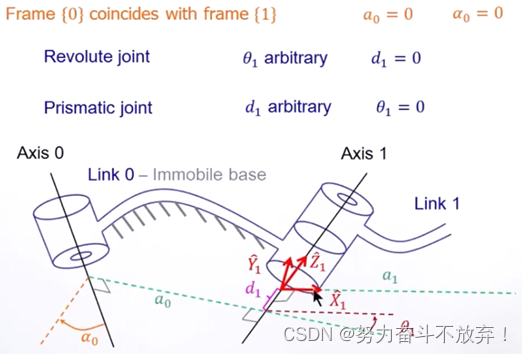
• 建立最后一个杆件link n刚体坐标系：
  ${\hat{X}}_n$和${\hat{X}}_{n-1}$同方向 $a_n=0$，${\alpha }_n=0$
  转动副时，坐标系建立在${\theta }_1$为变量，$d_n=0$时的位置，${\theta }_n=0$为初始位置
  移动副时，坐标系建立在$d_1$为变量，${\theta }_n=0$时的位置，$d_n=0$为初始位置
  

• 总结(craig version)：
  

1.4 Link trans

根据四个参数获取旋转矩阵${}_i^{i-1}T$
$${}_{}^{i-1}P={}_i^{i-1}T{}_{}^{i}P=T_{{\hat{X}}_{i-1}}\left({\alpha }_{i-1}\right)T_{{\hat{X}}_R}\left(a_{i-1}\right)T_{{\hat{Z}}_Q}\left({\theta }_i\right)T_{{\hat{Z}}_P}\left(d_i\right){}_{}^{i}P$$
$${}_i^{i-1}T=T_{{\hat{X}}_{i-1}}\left({\alpha }_{i-1}\right)T_{{\hat{X}}_R}\left(a_{i-1}\right)T_{{\hat{Z}}_Q}\left({\theta }_i\right)T_{{\hat{Z}}_P}\left(d_i\right)=\left[\begin{array}{cc}\begin{array}{cc}c{\theta }_i& -s{\theta }_i\\ s{\theta }_{i}c{\alpha }_{i-1}& c{\theta }_{i}c{\alpha }_{i-1}\end{array}& \begin{array}{cc}0& a_{i-1}\\ -s{\alpha }_{i-1}& -s{\alpha }_{i-1}{d}_i\end{array}\\ \begin{array}{cc}s{\theta }_{i}s{\alpha }_{i-1}& c{\theta }_{i}s{\alpha }_{i-1}\\ 0& 0\end{array}& \begin{array}{cc}c{\alpha }_{i-1}& c{\alpha }_{i-1}{d}_i\\ 0& 1\end{array}\end{array}\right]$$(属于欧拉角变换)
先沿着${\hat{X}}_{i-1}$转动${\alpha }_{i-1}$，使得两个转轴Z轴同向；再沿着${\hat{X}}_{i-1}$移动$a_{i-1}$，使得Z轴共线；再沿着${\hat{Z}}_i$转动${\theta }_i$，使得两个转轴X轴同向；再沿着${\hat{Z}}_i$移动$d_i$，使得坐标系重合。

连续link transformations：$${}_n^{0}T={}_1^{0}T{}_2^{1}T\cdots {}_{n-1}^{n-2}T{}_n^{n-1}T$$
上式可以理解为两种含义：

• Frame{n}相对于Frame{0}在空间中的位置和姿态

• Frame{n}中的向量转换到Frame{0}下表达

Example：

1.5 Actuator,Joint,Cartesian Space

正向运动学是轴空间到笛卡尔空间，逆向向运动学是笛卡尔空间到轴空间。
驱动器转动多少角度，轴将转动多少角度。如马达转多少，joint转多少，一般之间会有减速器，有个比例关系。减速器的作用是提供低转速高扭力。

驱动器空间到joint空间的例子(移动+转动的驱动)：

1.6 D-H表达法小结

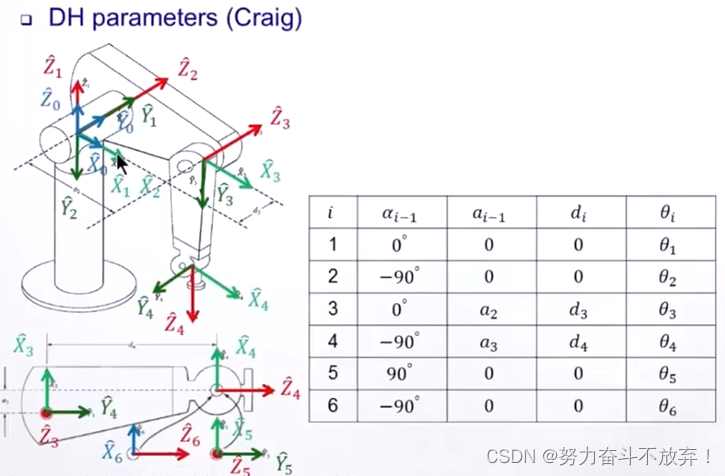
之前介绍的是D-H表达法(craig version)
D-H表达法(Standard version):在一些定义上与craig version存在差异，craig version获取得到最后一个关节的坐标系最终需要乘上一个向量P来获得最终抓取位置，而standard version直接获取到抓取位置的坐标系。
此时的齐次矩阵是先旋转${\theta }_i$，再移动$d_i$，再移动$a_i$，最后转动${\alpha }_i$ $${}_i^{i-1}T=T_{{\hat{Z}}_{i-1}}\left({\theta }_i\right)T_{{\hat{Z}}_R}\left(d_i\right)T_{{\hat{X}}_Q}\left(a_i\right)T_{{\hat{X}}_P}\left({\alpha }_i\right)=\left[\begin{array}{cc}\begin{array}{cc}c{\theta }_i& -s{\theta }_{i}c{\alpha }_i\\ s{\theta }_i& c{\theta }_{i}c{\alpha }_i\end{array}& \begin{array}{cc}s{\theta }_{i}s{\alpha }_i& a_{i}c{\theta }_i\\ -c{\theta }_{i}s{\alpha }_i& a_{i}s{\theta }_i\end{array}\\ \begin{array}{cc}0& s{\alpha }_i\\ 0& 0\end{array}& \begin{array}{cc}c{\alpha }_i& d_i\\ 0& 1\end{array}\end{array}\right]$$
示例1的standard version(左)和示例2 Craig version(右)：


实际过程中一定要像上图一样化简为最终代数式，减少矩阵中一些0元素的乘除给CPU带来开销，提高程序效率

二、逆向运动学

2.1 逆向运动学引言(inverse kinematic)

已知最终机械臂位姿，反算各关节角度。

假设手臂有6个自由度，就有6个未知角度。需要${}_H^{W}T$从中提取${}_6^{0}T=\left[\begin{array}{cc}{}_6^0{R}_{3\times 3}& {}_{}^0{P}_{6{org}_{3\times 1}}\\ \begin{array}{ccc}0& 0& 0\end{array}& 1\end{array}\right]$，需要求解

• 12个nonlinear transcendental equation(超越方程)
• 6个未知数，6个限制条件

Reachable workspace：能有一种以上的姿态到达空间中一个位置。
Dexterous workspace：能用任意姿态到达的位置。是Reachable workspace的子集。

灰色区域为Reachable workspace
红色的点为Dexterous workspace
Subspace：手臂在定义头尾的T所能到达的变动范围。

2.2 多重解

解的数目:

• 由于是非线性超越方程，6未知数6方程不代表有唯一解。
• 是由joint数目和link参数所决定的。

例如PUMA的多重解：

解析法：
  用代数或者几何的方法求解
数值法:
  数值分析的方法求解

大多数机械手臂采用解析解，因为解析解相较于数值解去逼近，计算速率更快。
一般后相邻三轴交于同一点会存在解析解(Pieper‘s solution)。

2.2 平面求逆解示例

几何法：将空间几何切割成平面几何。

代数法：

利用笛卡尔坐标系转到极坐标系来化简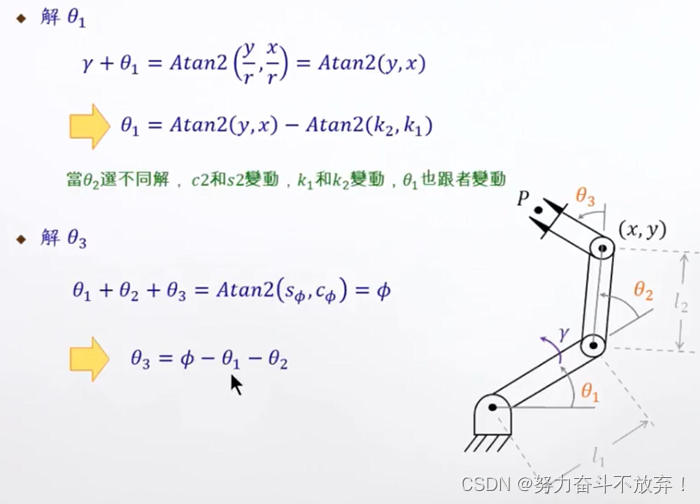

三角函数方程式求解：
例如如何求$acos\theta +bsin\theta =c$的$\theta$？

3.3 Pieper’s solution空间求逆解示例

6-DOF具有连续三轴交于同一点(一般为产生旋转的后三轴)，则手臂有解析解

$${{}_{}^{0}P}_{6org}={{}_{}^{0}P}_{4org}$$
接下来是机械臂移动部分的参数求解${\theta }_1，{\theta }_2，{\theta }_3$
从左到右从上到下为求解步骤1，2，3，4.


至此，机械臂移动部分的${\theta }_1，{\theta }_2，{\theta }_3$都求解获得。

接下来是转动部分的求解${\theta }_4，{\theta }_5，{\theta }_6$
公式：${}_6^{3}R={}_3^0{R}^{-1}{}_6^{0}R$
利用Z-Y-Z Euler angle 求解${\theta }_4，{\theta }_5，{\theta }_6$

DH定义下的解和Z-Y-Z Euler angle的解是相近的，下图解释原由。
DH的旋转是定义在以这个关节的旋转轴为轴线进行旋转。
Euler angle则是一路上都是沿着同一个坐标系坐标轴做旋转。

具体怎么求解${\theta }_4，{\theta }_5，{\theta }_6$视频内暂无该部分内容！！！

2.4 物体取放(手臂与目标)

求解出${\theta }_1，{\theta }_2，{\theta }_3，{\theta }_4，{\theta }_5，{\theta }_6$步骤如下

---

总结

以上就是所有的内容，本文包含正、逆运动学相关内容的笔记，接下来是轨迹规划部分内容的笔记。