一、本文简介

使用之前文章（参考3）中的数据，但是对非线性函数使用了无迹卡尔曼（UKF）来滤波。

二、环境

• 语言：julia 1.5
• 第三方包：DataFrames, CSV, LinearAlgebra, Plots, PyPlot, StatsBase, Distributions

三、参考

1. 多传感器数据融合及其应用－杨万海－西安电子科技大学出版社
2. 机器人学中的状态估计－高翔等译－西安交通大学出版社
3. 小市民：扩展卡尔曼滤波(EKF)代码实战

四、理论

此部分主要源于参考2 P103-105 中关于 sigmapoint卡尔曼滤波部分，其中依据P100中的描述，参数

，也可以网上自行搜索相关理论。

注：原问题是运动方程是线性，观测方程是非线性的，由于UKF在校正环节需要计算状态向量X和观测向量Y的协方差，因此将线性化的运动方程也进行了无迹变换。尚未搜到这种情况下的其余处理算法。

五、代码

#= 

六、结果

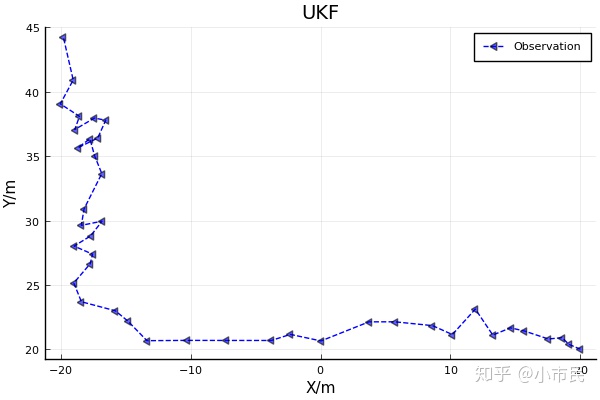
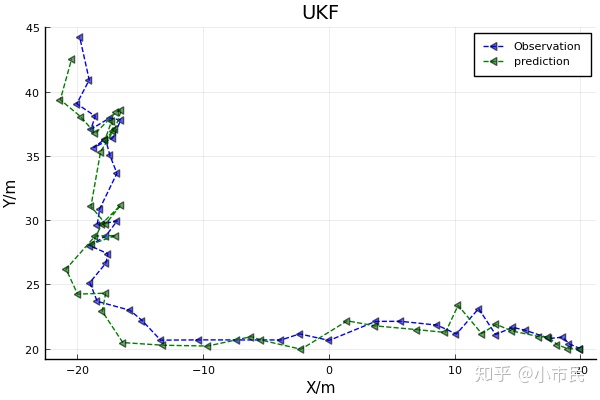
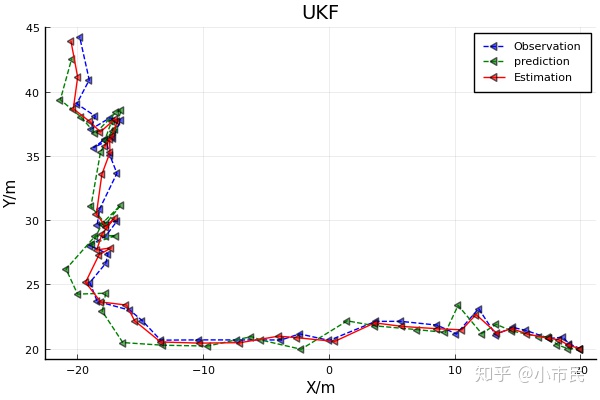
七、EKF和UKF的预测值和估计值对比

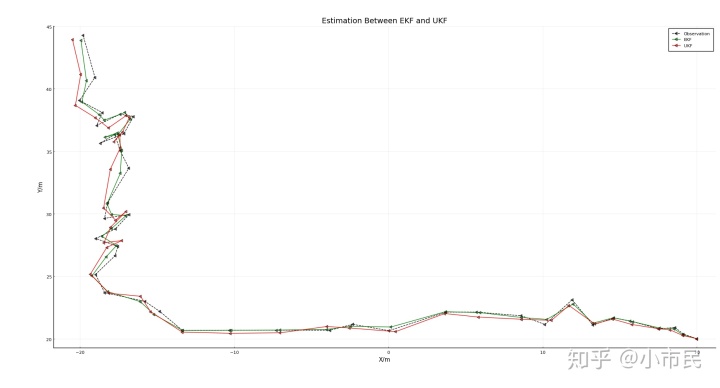
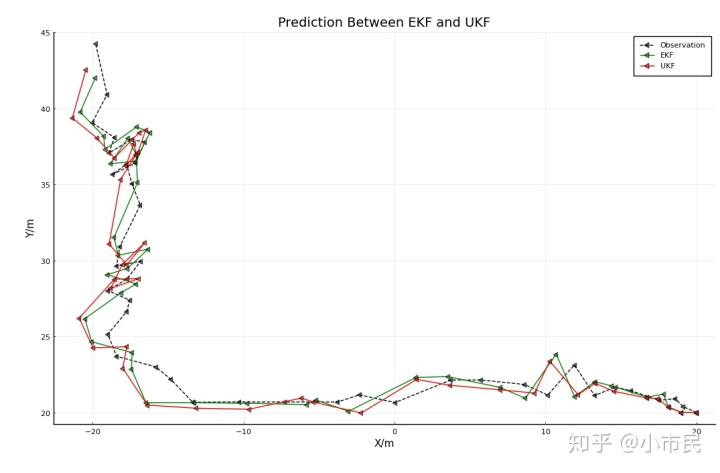
由图中可看出，差距并不是非常大