梯度下降与线性回归–《机器学习》课程学习笔记

什么是机器学习

机器学习的原始定义（Arthur Samuel）为在进行特定编程的情况下，给予计算机学习能力的领域。
在后来，卡内基梅隆大学的Tom Mitchell 将机器学习定义为：一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当有了经验E之后，经过P评判，程序在处理T时的性能有所提升。

学习的主要内容

这门课程的视野很宽，主要想将大家培养成出色的机器学习研究人员。
课程学习的主要内容有：

• 监督学习
• 非监督学习
• 学习理论
• 强化学习

监督学习(supervised learning)

监督学习是指导计算机进行学习，也就是告诉计算机什么样的Y是“正确答案”。

• 房屋销售价格问题
• 癌症诊断问题

分类问题与回归问题(classification and regression)

分类问题与回归问题的最大区别在于Y值的连续性与否。
分类问题的Y值是非连续的，例如 {0,1} <script type="math/tex" id="MathJax-Element-1">\{0,1\}</script>,如上述迭代癌症诊断，用0表示良性，用1表示恶性。
回归问题他的Y值是连续的，如上述房屋销售问题，它的取值是实数域上的一系列连续点。

非监督学习(unsupervised learning)

非监督学习我们没有人为给计算机告知什么是“正确答案”，让计算机自己来进行分析。
例如：

• DNA问题
• 声音剥离问题（聚类算法）

单变量线性回归(Linear Regression with one variable)

线性回归算法

描述回归问题的符号：

• m 代表训练集中实例的数量
• x 代表特征/输入变量
• y 代表目标变量/输出变量
• (x, y) 代表训练集中的实例
• (xi,yi) <script type="math/tex" id="MathJax-Element-2">(x^{i}, y^{i})</script>代表第i个观察实例
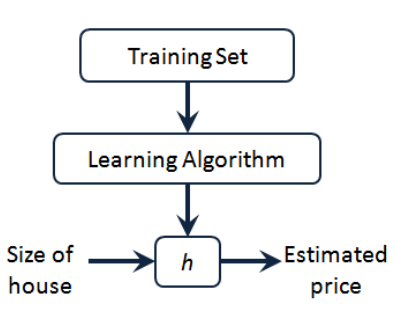
• h 代表学习算法的解决方案或者函数，也称为假设(hypothesis)

代价函数(Cost Function)

Hypothesis:
hθ(x)=θ0+θ1x <script type="math/tex" id="MathJax-Element-3">h_\theta(x)=\theta_0+\theta_1x</script>
Parameters:
θ0,θ1 <script type="math/tex" id="MathJax-Element-4">\theta_0,\theta_1</script>
Cost Function:
ȷ(θ0,θ1)=12m∑m1(hθ(x(i))−y(i))2 <script type="math/tex" id="MathJax-Element-5">\jmath(\theta_0,\theta_1)=\frac{1}{2m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2</script>
Goal:
minimizeθ0,θ1  ȷ(θ0,θ1) <script type="math/tex" id="MathJax-Element-6">minimize_{\theta_0,\theta_1} \ \ \jmath(\theta_0,\theta_1)</script>

梯度下降算法(Gradient descent algorithm)

repeat until convergence {
θj:=θj−αϑϑθjȷ(θ0,θ1)(forj=0andj=1) <script type="math/tex" id="MathJax-Element-7">\qquad \theta_j := \theta_j - \alpha\frac{\vartheta}{\vartheta\theta_j}\jmath(\theta_0,\theta_1)\qquad(for j = 0 and j = 1)</script>
}
Correct: Simultaneous update
temp0:=θ0−αϑϑθ0ȷ(θ0,θ1) <script type="math/tex" id="MathJax-Element-8">\qquad temp0 := \theta_0 - \alpha\frac{\vartheta}{\vartheta\theta_0}\jmath(\theta_0,\theta_1)</script>
temp1:=θ1−αϑϑθ1ȷ(θ0,θ1) <script type="math/tex" id="MathJax-Element-9">\qquad temp1 := \theta_1 - \alpha\frac{\vartheta}{\vartheta\theta_1}\jmath(\theta_0,\theta_1)</script>
θ0:=temp0 <script type="math/tex" id="MathJax-Element-10">\qquad\theta_0 := temp0</script>
θ1:=temp1 <script type="math/tex" id="MathJax-Element-11">\qquad\theta_1 := temp1</script>

注：
α <script type="math/tex" id="MathJax-Element-12">\alpha</script>是学习速度，如果其过慢则收敛所需要的时间会增加，若其过快，那么其可能越过了代价函数最小值点而不收敛。

线性回归算法(Linear Regression Algo)

Repeat {
θ0:=θ0−α1m∑m1(hθ(x(i)−y(i) <script type="math/tex" id="MathJax-Element-13">\qquad\theta_0:=\theta_0-\alpha\frac{1}{m}\sum_1^m(h_\theta(x^{(i)}-y^{(i)}</script>
θ1:=θ1−α1m∑m1(hθ(x(i)−y(i) <script type="math/tex" id="MathJax-Element-14">\qquad\theta_1:=\theta_1-\alpha\frac{1}{m}\sum_1^m(h_\theta(x^{(i)}-y^{(i)}</script>
}

注：
上述算法称之为批量梯度下降算法，顾名思义批量就是每次改变 θj <script type="math/tex" id="MathJax-Element-15">\theta_j</script>的值那么要将所有的m个样本进行求和。
我们将这种算法应用到线性回归中，那么就称之为线性回归的梯度下降算法，也叫作线性回归算法。

多变量线性回归(Linear Regression with multiple variables)

代价函数

Cost Function:
ȷ(θ0,θ1...θn)=12m∑m1(hθ(x(i))−y(i))2 <script type="math/tex" id="MathJax-Element-16">\jmath(\theta_0,\theta_1...\theta_n)=\frac{1}{2m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2</script>
hθ(x)=θTX=θ0x0+θ1x1+...+θnxn <script type="math/tex" id="MathJax-Element-17">h_\theta(x)=\theta^TX=\theta_0x_0+\theta_1x_1+...+\theta_nx_n</script>

多变量线性回归批量梯度下降算法

Repeat{ <script type="math/tex" id="MathJax-Element-18">Repeat \{</script>
θj:=θj−αϑϑθjȷ(θ0,θ1...,θn) <script type="math/tex" id="MathJax-Element-19">\qquad\theta_j:=\theta_j-\alpha\frac{\vartheta}{\vartheta\theta_j}\jmath(\theta_0,\theta_1...,\theta_n)</script>
} <script type="math/tex" id="MathJax-Element-20">\qquad\}</script>

也即：

Repeat{ <script type="math/tex" id="MathJax-Element-21">Repeat \{</script>
θj:=θj−αϑϑθj12m∑m1(hθ(x(i))−y(i))2 <script type="math/tex" id="MathJax-Element-22">\qquad\theta_j:=\theta_j-\alpha\frac{\vartheta}{\vartheta\theta_j}\frac{1}{2m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2</script>
} <script type="math/tex" id="MathJax-Element-23">\qquad\}</script>

求导后得到：

Repeat{ <script type="math/tex" id="MathJax-Element-24">Repeat \{</script>
θj:=θj−αϑϑθj1m∑m1(hθ(x(i))−y(i))∗x(i)j <script type="math/tex" id="MathJax-Element-25">\qquad\theta_j:=\theta_j-\alpha\frac{\vartheta}{\vartheta\theta_j}\frac{1}{m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})*x_j^{(i)}</script>
simultaneously  update  θj <script type="math/tex" id="MathJax-Element-26">\qquad \quad simultaneously\ \ update\ \ \theta_j</script>
} <script type="math/tex" id="MathJax-Element-27">\qquad\}</script>

梯度下降法实践

实践一：特征缩放(Feature Scaling)

在X中存在多个特征值的情况下，各个特征值之间的量程差异较大，导致使用梯度下降法进行线性回归的时候，可能根本就不会收敛或者收敛的速度相当慢。
因此要使用特征缩放的方法来使各个特征值的取值范围控制在[-1,1]之间，其实理论上而言[-3,3],[ 13,13 <script type="math/tex" id="MathJax-Element-28">\frac{1}{3},\frac{1}{3}</script>]都是一种很好的状态，只要是与[-1,1]相差不大即可。
另外实际上我们更加希望将其控制在[0.5,0.5]之间，因此使用 xn=xn−μnsn <script type="math/tex" id="MathJax-Element-29">x_n=\frac{x_n-\mu_n}{s_n}</script>
(其中 μn <script type="math/tex" id="MathJax-Element-30">\mu_n</script>是平均值， sn是标准差 <script type="math/tex" id="MathJax-Element-31">s_n是标准差</script>)

实践二：学习率(Learning Rate)

控制一个较好的 α <script type="math/tex" id="MathJax-Element-32">\alpha</script>的值是一个线性回归算法收敛的关键，如果 α <script type="math/tex" id="MathJax-Element-33">\alpha</script>的值过小，那么收敛的速度就会相当慢，而如果 α <script type="math/tex" id="MathJax-Element-34">\alpha</script>的值太大，那么总体上代价函数可能会随迭代次数增加而呈现出上升趋势或者是二次型函数，不会收敛。
通常，我们可以考虑以下学习率：

α=0.01,0.03,0.1,0.3,1,3,10 <script type="math/tex" id="MathJax-Element-35">\alpha=0.01,0.03,0.1,0.3,1,3,10</script>

特征与多项式回归(Features and Polynomial Regression)

有时候线性回归并不适用于所有的数据，我们需要使用曲线来适应我们的数据，比如一个二次方模型：

hθ(x)=θ0+θ1x1+θ2x22 <script type="math/tex" id="MathJax-Element-36">h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2</script>

或者是三次方模型来进行拟合：

hθ(x)=θ0+θ1x1+θ2x22+θ3x33 <script type="math/tex" id="MathJax-Element-37">h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3</script>

通常我们是先观察数据然后决定准备尝试怎样的模型，另外我们可以通过特征缩放与参数变换转化为：

hθ(x)=θ0+θ1(size)+θ2(size)2 <script type="math/tex" id="MathJax-Element-38">h_\theta(x)=\theta_0+\theta_1(size)+\theta_2(size)^2</script>

或者：

hθ(x)=θ0+θ1(size)+θ2(size)‾‾‾‾‾√ <script type="math/tex" id="MathJax-Element-39">h_\theta(x)=\theta_0+\theta_1(size)+\theta_2\sqrt{(size)}</script>

正规方程(Normal Equation)

使用正规方程的求解方法对于解决特征数目小于10000的情况下，由于其只需要一次计算，梯度下降需要多次迭代，因此收敛速度很快，则这个时候使用正规方程方法更占优势，而如果特征数目大于10000时，由于求矩阵的逆运算量过大，这个时候一般使用梯度下降算法。

正规方程通过求解下面的方程来找出使得代价函数最小的参数：
ϑϑθjȷ(θj)=0,ȷ(θ)=aθ2+bθ+c <script type="math/tex" id="MathJax-Element-40">\frac{\vartheta}{\vartheta\theta_j}\jmath(\theta_j)=0\qquad,\jmath (\theta)=a\theta^2+b\theta+c</script>
可以解得：
θ=(XTX)−1XTy <script type="math/tex" id="MathJax-Element-41">\theta=(X^TX)^{-1}X^Ty</script>

向量化(Vectorization)

使用合适的向量化方法可以大大简化计算，比用一个for循环好用许多。

求解如下的线性回归函数：
hθ(x)=∑nj=0θjxj <script type="math/tex" id="MathJax-Element-42">h_\theta(x)=\sum_{j=0}^{n}\theta_jx_j</script>

Unvectorized implementation
prediction = 0.0;
for j = 1:n+1,
    prediction = prediction + theta(j) * x(j)
end;

Vectorized implementation
prediction = theta' * x;

下面来分析一个比较复杂的例子—–线性回归算法梯度下降的更新规则

θ0:=θ0−αϑϑθj1m∑m1(hθ(x(i))−y(i))x(i)0 <script type="math/tex" id="MathJax-Element-43">\theta_0:=\theta_0-\alpha\frac{\vartheta}{\vartheta\theta_j}\frac{1}{m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}</script>
θ1:=θ1−αϑϑθj1m∑m1(hθ(x(i))−y(i))x(i)1 <script type="math/tex" id="MathJax-Element-44">\theta_1:=\theta_1-\alpha\frac{\vartheta}{\vartheta\theta_j}\frac{1}{m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})x_1^{(i)}</script>
θ2:=θ2−αϑϑθj1m∑m1(hθ(x(i))−y(i))x(i)2 <script type="math/tex" id="MathJax-Element-45">\theta_2:=\theta_2-\alpha\frac{\vartheta}{\vartheta\theta_j}\frac{1}{m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})x_2^{(i)}</script>

如果使用for循环同样会增大程序复杂度以及运行时间，我们可以采用以下的向量化算法：

Vectorized implementation
θ:=θ−αδ <script type="math/tex" id="MathJax-Element-46">\theta:=\theta-\alpha\delta</script>
δ=1m∑mi=1((hθ(x(i))−y(i))x(i)) <script type="math/tex" id="MathJax-Element-47">\delta=\frac{1}{m}\sum_{i=1}^{m}((h_\theta(x^{(i)})-y^{(i)})x^{(i)})</script>