模式识别——统计决策方法——最小错误率贝叶斯决策

内容参考《模式识别》张学工

引言

问题背景

假定我手单握着一枚硬币，让你着是多少钱的硬币，这其实就可以看作一个分类决策的
问题：你需要从各种回能的硬币中作出一个决策。如果我告诉你这枚硬币只可能是一角或
者五角，这就是一个两类的分类问题。

数学问题

把硬币的重量仍记为x，与上面所述的决策过程类似，现在应该考查在已知这枚硬币重量为x情况下硬币属于各类的概率，对两类硬币分别记作$P(w_1|x)和P(w_2|x)$，这种概率称作后验概率：这时的决策规则应该是
$$如果P(w_1|x)>P(w_2|x)，则x\in w_1；反之x\in w_2$$
根据概率论中的贝叶斯公式，有
$$P(w_1|x)=\frac{p(x,w_1)}{p(x)}=\frac{p(x|w_1)P(w_1)}{p(x)},i=1,2$$
其中，$P(w_1)$是先验概率；$p(x,w_1)$是x与$w_1$的联合概率密度；p(x)是两类所有硬币重量的概率密度，称作总体密度：$p(x|w_1)$是第i类硬币重量的概率密度，称为类条件密度。这样，后验概率就转换成先验概率与类条件密度的乘积，再用总体密度进行归一化

若对于前验概率，后验概率等概念不是很理解的，可以去参考https://zhuanlan.zhihu.com/p/38567891

最小错误率贝叶斯决策

最小错误率决策

正如在前面例子中看到的，在一般的模式识别问题中，人们往往希望尽量减少分类
的错误，即目标是追求最小错误率。从最小错误率的要求出发，利用概率论中的贝叶斯公式，就能得出使错误率最小的分类决策，称之为最小错误率贝叶斯决策。
$$minP(e)=\int P(e|x)p(x)dx$$
其中$P(e|x)$是对单个样本x的决策总体错误率，包括将正类x决策为负类，将负类x决策为正类，而$p(x)$则是x的分布概率，将这两个式子相乘积分得到就是所有样本的平均错误率。也就是我们要最小化的目标。

因为
$$\begin{array}{rl}P(e|x)& =P(w_1|x),决策x\in w_2\\ & =1-P(w_2|x),决策x\in w_2\\ & 此处的P(w_2|x)为我们所求的后验概率\end{array}$$
对于$P(e|x)=P(w_2|x),决策x\in w_1$同理，因此最小化错误率可以转化为最大化后验概率

最大化后验概率决策

决策规则变为
$$\begin{gathered} 如果P(w_1|x)>P(w_2|x)，则x\in w_1；反之,x\in w_2 \\ 其中后验概率为 \\ P(w_1|x)=\frac{p(x|w_1)P(w_1)}{p(x)}=\frac{P(x|w_1)p(x)}{{\sum }_{i=1}^{2}p(x|w_i)P(w_i)} \end{gathered}$$
如上式所述，两类分母相同，都是x的总体分布概率，因此要找到最大后验概率只需比较分子大小即可

比较方式1：类条件密度与前验概率乘积

谁最大选谁
$$若p(x|w_i)P(w_i)=ma{x}_{i=1,2}p(x|w_i)P(w_i),则x\in w_i$$

比较方式2：比较似然比（类条件密度之比）阈值

$$若l(x)=\frac{p(x|w_1)}{p(x|w_2)}\{\begin{array}{ll}>\frac{P(w_2)}{P(w_1)}& \text{则x∈w1}\\ <\frac{P(w_2)}{P(w_1)}& \text{则x∈w2}\end{array}$$

对似然概念不熟悉的同学可以参考https://blog.csdn.net/weixin_44731847/article/details/127337792

比较方式3：比较似然比阈值的对数形式

$h(x)=-ln[l(x)]=-lnp(x|w_1)+lnp(x|w_2)$

决策规则变为
$$若h(x)\{\begin{array}{ll}>ln\frac{P(w_1)}{P(w_2)}& \text{则x∈w1}\\ <ln\frac{P(w_1)}{P(w_2)}& \text{则x∈w2}\end{array}$$

错误率的进一步理解

利用贝叶斯公式，我们可以通过在不同类别下观测x，将类别的先验概率$P(w_i)$转换为后验概率$P(w_i|x)$

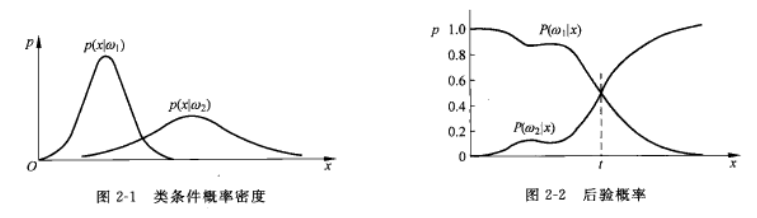
​ 从图2-2可以看到，这种决策实际的分界线是图中的虚线位置，如果样本x落在分界线左侧则归为第一类，落在右侧则归为第二类。这一分界线称作决策边界或分类线，在多维情况下称作决策面或分类面，它把特征空间划分成属于各类的区域。
​ 我们来分析一下错误率。决策边界把x轴分割成两个区域，分别称为第一类和第二类的决策区域${\mathcal{R}}_1\mathcal{和}{\mathcal{R}}_2$。${\mathcal{R}}_1$为$(-\infty ,t)$，${\mathcal{R}}_2$为$(t,\infty )$。样本在${\mathcal{R}}_1$中但属于第二类的概率和样本在${\mathcal{R}}_2$中但属于第一类的概率就是出现错误的概率，再考虑到样本自身的分布后就是平均错误率
$$\begin{array}{rl}P(e)& ={\int }_{-\infty }^{t}P(w_2|x)p(x)dx+{\int }_t^{\infty }P(w_1|x)p(x)dx\\ & 单个样本的后验概率\ast 样本总体分布，再积分\\ & ={\int }_{-\infty }^{t}p(x|w_2)P(w_2)dx+{\int }_t^{\infty }p(x|w_1)P(w_1)dx\\ & 每个类别观测x的似然度\ast 每个类别的先验概率，再积分\end{array}$$
其中
$$P_1(e)={\int }_{\mathcal{R}2}p(x|w_1)dx$$
是把第一类样本决策为第二类的错误率，称为第一类错误率
$$P_2(e)={\int }_{\mathcal{R}1}p(x|w_2)dx$$
是把第二类样本决策为第一类的错误率，称为第二类错误率

两类错误率用先验概率加权求和就是总的平均错误率

课本例题

假设在某个局部地区细胞识别中正常$(w_1)$和异常$(w_2)$两类的先验概率分别为
正常状态$P(w_1)=0.9$异常状态$P(w_2)=0.1$
现有一待识别的细胞，其观察值为x，从类条件概率密度曲线上分别查得
$p(x|w_1)=0.2,p(x|w_2)=0.4$
试对这细胞了进行分类

比较后验概率（x的总体分布对于两个类别而言相等）
$$\begin{array}{rl}P(w_1|x)& \to p(x|w_1)P(w_1)\\ & =0.2\times 0.9=0.18\\ P(w_2|x)& \to p(x|w_2)P(w_2)\\ & =0.4\times 0.1=0.04\end{array}$$
0.18>0.04，所以x属于正常类