图像处理基础—学习笔记

图像增强图像增强的目的是通过对图像中的信息进行处理，使得有利于模式识别的信息得到增强，不利于模式识别的信息被抑制，扩大图像中不同物体特征之间的差别，为图像的信息提取及其识别奠定良好的基础。图像增强的方法按照实现方法不同可以分为点增强、空域增强和频域增强。点增强主要指图像灰度变换和几何变换。图像灰度变换也称为点运算、对比度增强或对比度拉伸，它是图像数字化软件和图像显示软件的重要组成部分。灰度...

studyeboy

932人浏览 · 2019-07-09 16:20:59

studyeboy · 2019-07-09 16:20:59 发布

文章目录

颜色空间

色彩空间与色彩模型都是一种用数值表示颜色的数学模型。其中色彩空间侧重于色彩的标识，色彩模型侧重色彩的生成。
从面向对象主要分为两大类模型：面向硬件设备的色彩模型和面向视觉感知的色彩模型。
面向设备的色彩模型有：RGB、CMYK、YUV
面向视觉感知的色彩模型有：HSV、Lab

RGB颜色空间

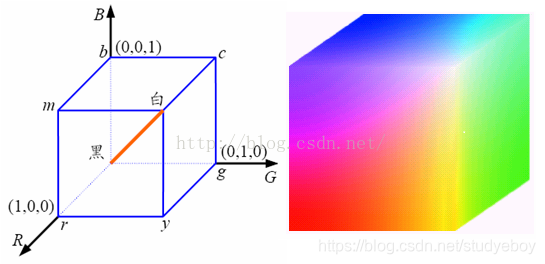
RGB颜色空间是基于物体发光定义的（RGB正好对应光的三原色：Red，Green，Blue），基于颜色的加法混色原理，从黑色不断叠加Red、Green，Blue的颜色，最终可以得到白色光。将R、G、B三个通道作为笛卡尔坐标系中的X、Y、Z轴，就得到了一种对于颜色的空间描述。常用于电视、摄像机和彩色扫描仪等显示器的色彩模型。缺点是色彩空间不够均匀，不够直观，不符合人的认知心理，即颜色间的认知差异不能用空间上两点的距离来表示。
在这里插入图片描述

CMYK颜色空间

CMYK颜色空间是基于光反射定义的（CMYK对应了绘画中的三原色：青Cyan，品红Magenta，黄Yellow，黑black，为了避免与蓝色混淆，黑色用K表示。），是另一种基于颜色减法混色原理的颜色模型。在工业印刷中描述的是需要在白色介质上使用何种油墨，通过光的反射显示出颜色的模型。CMYK描述的是青、品红、黄和黑四种油墨的数值。CMYK颜色空间的颜色值与RGB颜色空间中的取值可以通过线性变换相互转换。
在这里插入图片描述

YUV颜色空间

在现代彩色电视系统中，通常采用三管彩色摄像机或彩色CCD（点耦合器件）摄像机，它把获得的彩色图像信号，经分色、分别放大校正得到RGB，再经过矩阵变换电路得到亮度信号Y和两个色差信号R-Y、B-Y，最后发送端将亮度和色差三个信号分别进行编码，用同一信道发送出去。这就是我们常用的YUV空间，采用YUV色彩空间的重要性是它的亮度信号Y和色度信号U、V是分离的。如果只有Y信号分量而没有U、V分量，那么表示的图就是黑白灰度图。彩色电视采用YUV空间正是为了用亮度信号Y解决彩色电视机与黑白电视机的兼容问题，使黑白电视机也能接收彩色信号。根据美国国际电视制式委员会，NTSC制式的标准，当白光的亮度用Y表示时，它和红、绿、蓝三色光的关系可用 $Y = 0.3 R + 0.59 G + 0.11 B$ 亮度公式描述，色差U、V是由B-Y、R-Y按不同比例压缩而成的。如果要由YUV空间转化成RGB空间，只要进行相反的逆运算即可。与YUV色彩空间类似的还有Lab色彩空间，它也是用亮度和色差来描述彩色分量，其中L为亮度、a和b分别为各色差分量。

HSV模型

HSV颜色空间是根据颜色的直观特性创建的一种颜色空间，也称六角椎体模型。RGB和CMYK颜色模型都是面向硬件的，HSV是面向用户的。HSV模型更符合人描述和解释颜色的方式，HSV的彩色描述对人来说是自然且非常直观的。H分量基本能表示一个物体的颜色，但是S和V的取值也要在一定范围内，因为S代表的是H所表示的那个颜色和白色的混合程度，S越小，颜色越发白，也就越浅；V代表的是H所表示的那个颜色和黑色的混合程度，V越小，颜色越发黑。

色调（H：hue）角度度量，取值范围为0°~360°，从红色开始按逆时针方向计算，红色为0°（对应补色青色为180°），绿色为120°（对应补色为品红色300°），蓝色为240°（对应补色为黄色为60°）。色调决定一个像素点中的颜色偏向于哪一种颜色。
饱和度（S：saturation）取值范围为0.0~1.0，饱和度决定了颜色空间中颜色分量，饱和度越高，说明颜色越深，饱和度越低，说明颜色越浅。饱和度在颜色空间中起到一个控制RGB组合色的颜色深度的作用。
亮度（V：value）取值范围为0（黑色）~255（白色）。亮度决定颜色空间中颜色的明暗程度。

HSV模型的三角维表示从RGB立方体演化而来。从RFB沿立方体对角线的白色顶点向黑色顶点观察，就可以看到立方体的六边形外形。六边形边界表示色彩，水平轴表示纯度，明度沿垂直轴测量。与加法减法混色的术语相比，使用色相，饱和度等概念描述色彩更自然直观。
OpenCV中HSV的取值范围
- COLOR_BGR2HSV参数下： H：0-180，S：0-255，V：0-255
- COLOR_BGR2HSV_FULL参数下：
  H：0-255， S：0-255， V：0-255

Lab颜色空间

Lab颜色空间是由CIE（国际照明委员会）制定的一种色彩模式。自然界中任何颜色都可以在Lab空间中表达出来，它的色彩空间比RGB空间还要大。这种模式是以数字化方式来描述人的视觉感应，与设备无关，弥补了RGB和CMYK模式必须依赖于设备色彩特性的不足。Lab颜色接近人类视觉，致力于感知均匀性，它的L分量密切匹配人类亮度感知。因此可以被用来通过修改a和b分量的输出色阶来做精确的颜色平滑，或使用L分量来调整亮度对比。

L 亮度
a 正数表示红色，负数表示绿色
b 正数表示黄色，负数表示蓝色

图像主色彩

对于一张RGB色彩空间的彩色图像，在色彩交界处都是通过像素混合来实现自然过渡，所以直接扫描图像的像素值，得到的不同颜色值可能多达上百种，而实际上图像可能只有3-4种主要色彩，如何去掉那些混合颜色，准确的提取出来图像的主色彩，根据一般图像的特征，图像在不同色彩的边界处混合不同的颜色值，此可以视为图像的边缘特性之一，因此可以根据简单的边缘梯度算法实现这些混合像素的提取得到输出的像素值数组，然后扫描每个像素值，寻找指定半径参数R周围的像素，发现为零，而且距离中心像素最近的像素点的值作为中心像素的像素值，扫描结束后输出像素数组，然后对数组线性扫描，即可得到图片的主要色彩RGB值。
算法步骤

输入图像数组，对彩色图像灰度化。
对灰度图像，计算图像梯度。
对得到的每个非零像素点实现半径为R（参数根据不同应用场景，找到最合适的值，理论上图像越大，R的取值应该越大，否则算法会失准）的范围内的扫描，找出与之最相近的为零的原像素值。
对得到的数组进行简单的扫描，得到主色彩。

图像增强

图像增强的目的是通过对图像中的信息进行处理，使得有利于模式识别的信息得到增强，不利于模式识别的信息被抑制，扩大图像中不同物体特征之间的差别，为图像的信息提取及其识别奠定良好的基础。图像增强的方法按照实现方法不同可以分为点增强、空域增强和频域增强。

点增强主要指图像灰度变换和几何变换。图像灰度变换也称为点运算、对比度增强或对比度拉伸，它是图像数字化软件和图像显示软件的重要组成部分。
灰度变换是一种既简单又重要的技术，它能让用户改变图像数据占据的灰度范围。一幅输入图像经过灰度变换后将产生一幅新的输出图像，由输入像素点的灰度值决定相应的输出像素点的灰度值。灰度变换不会改变图像内的空间关系。
图像的几何变换是图像处理中的另一种基本变换。它通常包括图像的平移、图像的镜像变换、图像的缩放和图像的旋转。通过图像的几何变换可以实现图像的最基本的坐标变换及缩放功能。
空间增强 图像的空间信息可以反应图像中物体的位置、形状、大小等特征，而这些特征可以通过一定的物理模式来描述。例如，物理的边缘轮廓由于灰度值变换剧烈一般出现高频率特征，而一个比较平滑的物体内部由于灰度值比较均一则呈现低频率特征。因此，根据需要可以分别增强图像的高频和低频特征。对图像的高频增强可以突出物体的边缘轮廓，从而起到锐化图像的作用。相应的，对图像的低频部分进行增强可以对图像进行平滑处理，一般用于图像的噪声消除。
频域增强 图像的频域增强一般只是对数字图像进行局部增强，而图像的频域增强可以对图像进行全局增强。频域增强技术是在数字图像的频域空间对图像进行滤波，因此需要将图像从空间域变换到频率域，一般通过傅里叶变换实现。在频率域空间的滤波与空域滤波一样可以通过卷积实现，因此傅里叶变换和卷积理论是频域滤波技术的基础。

图像纹理

灰度共生矩阵

灰度共生矩阵(Gray-level Co-occurrence Matrix, GLCM)，在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下，提出的具有广泛性的纹理分析方法。指的是一种通过研究灰度的空间相关性来描述纹理的常用方法。假设原图的灰度级为 $L$ ，那么灰度共生矩阵是 $L\times L$ 大小的计数矩阵。

共生矩阵用两个位置的像素的联合概率密度来定义，它不仅反映亮度的分布特征，也反映具有相同亮度或者接近亮度的像素之间的位置分布特征，是有关图像亮度变化的二阶统计特征。它是定义一组纹理特征的基础。

由于纹理是灰度在空间位置上反复出现而形成的，因而在图像空间中像个某距离的两像素之间会存在一定的灰度关系，即图像中灰度的空间相关性。灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法。

像素灰度在空间位置上的反复出现形成图像的纹理，GLCM是描述具有某种空间位置关系两个像素灰度的联合分布。

对于纹理变化缓慢的图像，其灰度共生矩阵对角线上的数值较大；而对于纹理变化较快的图像，其灰度共生矩阵对角线上的数值较小，对角线两侧的值较大。由于灰度共生矩阵的数据量较大，一般不直接作为区分纹理的特征，而是基于它构建的一些统计量作为纹理分类特征。Haralick曾提出14种基于灰度共生矩阵计算出来的统计量：即：能量、熵、对比度、均匀性、相关性、方差、和平方、和方差、和熵、差方差、差平均、差熵、相关信息测到以及最大相关系数。

在图像中任意一点（x,y）及偏离它的一点(x+a,y+b)(其中a，b为整数，认为定义)构成点对。设该点对的灰度值为(f1,f2),假设图像的最大灰度级为L,则f1与f2的组合共有L*L种。对于整福图像，统计每一种(f1,f2)值出现的次数，然后排列成一个方阵，再用(f1,f2)出现的总次数将它们归一化为出现的概率P(f1,f2)，由此产生的矩阵为灰度共生矩阵。

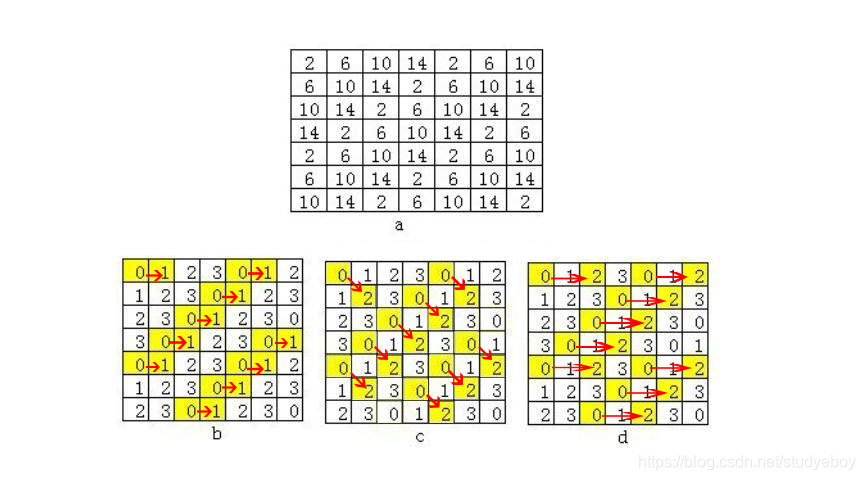
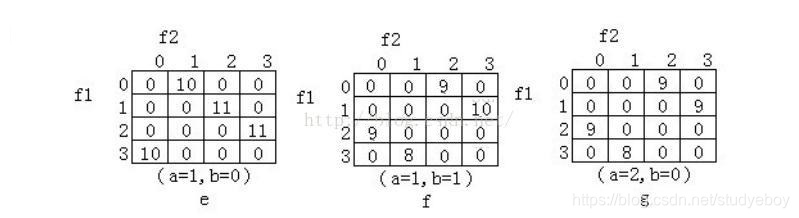
在这里插入图片描述

灰度共生矩阵的特征参数

图像的灰度矩阵反映图像视觉信息，而灰度共生矩阵则反映图像方向，相邻间隔、变化幅度的综合信息。通过统计灰度共生矩阵提取局部模式和排列规则，定义了14个用于纹理分析的灰度共生矩阵特征参数。

能量（Energy），也叫角二阶矩（Angular Second Moment）是灰度共生矩阵各元素值的平方和，是对图像纹理的灰度变化稳定程度的能量，反映了图像灰度分布均匀程度和纹理粗细度。能量值大表明当前纹理是一种规则变化较为稳定的纹理。
熵（Entropy）是图像包含信息量的随机性度量。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大，因此熵值表明了图像灰度分布的复杂程度，熵值越大，图像越复杂。
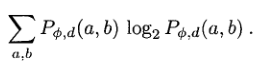
最大概率（Maximum probability）表示图像中出现次数最多的纹理特征。
对比度（Contrast）度量矩阵的值是如何分布和图像中局部变化的多少，反映了图像的清晰度和纹理的沟纹深浅。纹理的沟纹越深，反差越大，效果清晰；反之，对比值小，则沟纹浅，效果模糊。下面公式，典型的有 $k = 2$ ， $\lambda=1$ .
倒数差分数或逆差踞（Inverse difference moment），也叫同质度（Homogeneity），反映图像纹理的同质性，度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化，局部非常均匀。
相关性（Correlation）自相关反映了图像纹理的一致性，如果图像中有水平方向纹理，则水平方向共生矩阵Correlation值大于其余方向共生矩阵Correlation的值。它度量空间灰度共生矩阵元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时，相关性就大；相反，如果矩阵元素值相差很大则相关值小。

其中 $\mu_{x},\mu_{y}$ 为均值， $\sigma_{x}, \sigma_{y}$ 为方差。

scikit-image函数

计算灰度共生矩阵
灰度级共生矩阵是图像上给定偏移处的共生灰度值的直方图。

skimage.feature.greycomatrix(image, distances, angles, levels=None, symmetric=False, normed=False)

参数

image array_like整型输入图像。只支持正值图像。如果type不是uint8，则需要设置参数级别。
distances array_like像素对距离偏离列表。
angles array_like以弧度表示的像素对角列表。
levels int可选输入图像对应该包含0和level-1的整数，其中level指示计数的灰度数（对于8位图像通常为256）。该参数对于16位或更高的图像是必需的，通常是图像额最大值。由于输出矩阵至少为x水平，因此可能最好使用输入图像的分档而不是较大的水平值。
symmetric bool可选，如果为True，则输出矩阵P[:,:,d,theta]是对称的。这是忽略值对的顺序来实现的，所以（i，j）和（j，i）在给定偏移量时遇到（i，j）时被累加。默认值是False。
normed bool 可选，如果为True，则将每个矩阵P[:,:,d,theta]除以给定偏移量的累计同现事件总数。结果矩阵的元素总和为1，默认值为False。

P 4-D ndarray灰度共生直方图。值p（i，j，d，theta）是灰度级j在距离d和与灰度级i成角度 $\theta$ 时出现的次数。如果normed为False，则输出为uint32类型，否则为float64。尺寸是水平x水平x距离数量x角度数量。

例子
在这里插入图片描述

from skimage.feature import greycomatrix
import numpy as np
image = np.array([[0,0,1,1],[0,0,1,1],[0,2,2,2],[2,2,3,3]],dtype=np.uint8)
result = greycomatrix(image, [1], [0, np.pi/4, np.pi/2, 3*np.pi/4], levels=4)
print(type(result))
<class 'numpy.ndarray'>
print(result.shape)
(4, 4, 1, 4)
result[:,:,0,0] #p（1,0）
Out[24]: 
array([[2, 2, 1, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 1],
       [0, 0, 0, 1]], dtype=uint32)
result[:,:,0,1] # p（1,45）
Out[25]: 
array([[1, 1, 3, 0],
       [0, 1, 1, 0],
       [0, 0, 0, 2],
       [0, 0, 0, 0]], dtype=uint32)
result[:,:,0,2] # p（1,90）
Out[26]: 
array([[3, 0, 2, 0],
       [0, 2, 2, 0],
       [0, 0, 1, 2],
       [0, 0, 0, 0]], dtype=uint32)
result[:,:,0,3] # p（1,135）
Out[27]: 
array([[2, 0, 0, 0],
       [1, 1, 2, 0],
       [0, 0, 2, 1],
       [0, 0, 0, 0]], dtype=uint32)

计算GLCM的纹理属性
计算灰度共生矩阵的特征以作为矩阵的紧凑总结。

skimage.feature.greycoprops(P, prop='contrast')

参数

P ndarray输入数组。P是计算指定属性的灰度共生直方图。值P[i,j,d,theta]是灰度级j和i在距离为d角度为 $\theta$ 时出现的次数。
prop 可选GLCM的特性来计算，默认值是’contrast’
- contrast 对比度
- dissimilarity 非相似性
- homogeneity 同质度，也叫逆差踞或倒数差分数
- energy 能量
- correlation 相关性
- ASM 角二阶矩（Angular Second Moment）

计算公式

‘contrast’: $\sum_{i,j=0}^{levels-1} P_{i,j}(i-j)^2$
‘dissimilarity’: $\sum_{i,j=0}^{levels-1}P_{i,j}|i-j|$
‘homogeneity’: $\sum_{i,j=0}^{levels-1}\frac{P_{i,j}}{1+(i-j)^2}$
‘ASM’: $\sum_{i,j=0}^{levels-1} P_{i,j}^2$
‘energy’: $\sqrt{ASM}$
‘correlation’:
$\sum_{i,j=0}^{levels-1} P_{i,j}[\frac{(i-\mu_i) \\ (j-\mu_j)}{\sqrt{(\sigma_i^2)(\sigma_j^2)}}]$

例子

from skimage.feature import greycomatrix, greycoprops
image = np.array([[0,0,1,1],[0,0,1,1],[0,2,2,2],[2,2,3,3]], dtype=np.uint8)
image
Out[30]: 
array([[0, 0, 1, 1],
       [0, 0, 1, 1],
       [0, 2, 2, 2],
       [2, 2, 3, 3]], dtype=uint8)
g = greycomatrix(image, [1,2], [0,np.pi/2], levels=4, normed=True, symmetric=True)
contrast = greycoprops(g, 'contrast')
contrast
Out[34]: 
array([[0.58333333, 1.        ],
       [1.25      , 2.75      ]])