Dennis Ritchie的主页：http://cm.bell-labs.com/who/dmr/index.html

“他出生，他工作，他走了。” ——海德格尔

10.9.他走了，在此缅怀一下，感谢他做出的杰出贡献。

这个系列最初的几篇文章主要注重的是算法的复杂度分析和一些设计方面需要考虑的东西，问题本身不会太难，但随着复杂度分析的深入理解和掌握将逐渐面向高级数据结构（堆、树以及图）以及算法（DP、NP问题等）的分析。

问题：向量x中存在n个带符号整数（或浮点数），输出向量中元素之和为最大的任意连续子向量，即分别给出上下边界lowbound、highbound使其中的元素之和比任意其他的边界对中的元素之和都大。

问题的来源：问题最初的形式是一个二维数组，最大总和子数组为数字图像处理中某种特定模式的最大似然估计量，因为二维问题本身比较麻烦，故将其简化作为一个例子来将注意力转移至算法设计及分析方面的问题。

方法一：一看到这个问题我们都会想到的最简单的方法就是遍历整个向量，求出每个子向量之和并将其与其他和值进行比较。因此可简单写出：

设T(n)为算法的运行时间，则有：

由T(n)可知其运行时间与n的立方渐进等同，因此该算法在运行时间上的性能极差。

方法二：在方法一的基础上稍作思考，我们就能发现在方法一中嵌套的第三层循环其实是可以避免的，没错，方法一进行了多次重复计算，这导致它的性能变得极差，由此可做的修改如下：

同样进行算法的运行时间复杂度分析可得：

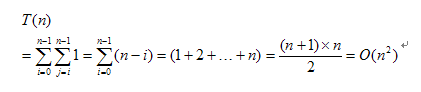
由此可知方法一的变种的运行时间与n的平方渐进等同，方法一的稍作改变即换来在输入规模n→∞时的性能的极大提升。再深入比较方法一和方法二可以发现带来改变的仅仅是内层循环中对前一计算状态的记录。形式化地说：对向量x[i..j]，计算其和为sum，那么对向量x[i..j+1]，其和可在sum的基础上加上x[j+1]得出，而方法一则是对x[i..j+1]中的所有元素再次进行重新计算，由此带来了极大的资源浪费。因此可知，算法设计中，在某个方面的观察乃至深入理解可以带来整个系统中局部性能的极大跃升。比如通过观察数据之间的联系重新选择数据结构，通过使用额外的空间进行状态的记录等等。

方法三：这一方法利用了分治算法的思想。分治算法的原理为：要解决规模为n的问题，可递归的解决两个规模近似为n/2的子问题，然后对它们的答案进行合并以得到整个问题的答案。由问题的性质，即“所寻找的子向量为连续的”入手，设定指针Ptr=(L+H)/2将整个向量一分为二，而我们所要找的子向量必定在以下三种情况中：

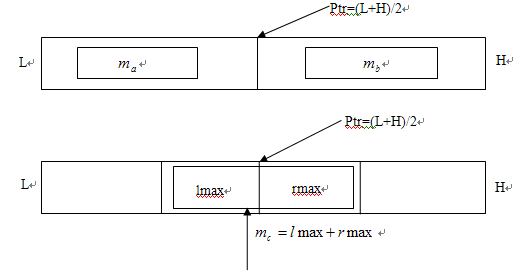
即和值最大的子向量或者在指针Ptr的左半边，或者在右半边，或者是左半边和右半边的最大值所在子向量所合并而成的向量。当然，细心的读者肯定会发现上图是有一些问题的，但我们只是泛化地表述一下分治的这种思想，这并不影响我们给出最终的解决方案。另一方面，既然对原问题进行了分解，那么递归的边界是什么呢？要清楚的解释何时递归将会返回，考虑存在两个元素的向量，由分治思想最终将两个元素的单个向量分解为两个存在一个元素的向量，此时和值最大的子向量或者是两个各存在一个元素的子向量，或者是整个向量，因此我们返回的即是当边界L=H时该下标所对应的元素值。(递归版本存在一个缺陷，因为在初次调用这个函数时无法确定子向量是否将被指针Ptr一分为二，同时在进行深层递归的过程中无法对边界状态进行记录并返回，因此就导致了该版本的函数只能求出子向量的和值，而无法准确记录子向量的边界。)由此：

同样对其进行复杂度分析，由于在maxsum函数体内调用其自身，据ptr=(l+h)/2以及return语句中的maxsum(l,ptr)和maxsum(ptr+1,h)可知该函数的调用将使用其自身形成一棵完整二叉树，用递归式表示为T(n)=2T(n/2)+O(n) 。（对递归式的分析参见主定理，这里直接引用其结论。）于是由主定理第二种情况可得：

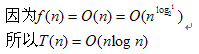
可以发现其性能比第二种方法更进一步，渐进紧确于O(nlogn)。

方法三是目前为止运行速度最快的算法，其由来已在上文说明。那么是否还存在一种方法，能达到运行时间复杂度的极限O(n)：即通过一次扫描检测即能断定和值最大的子向量及其上下界呢？这看起来不可思议，难道所有子向量在一次扫描之后即能比较完毕？是的，从某种意义上，我认为这要归功于它是“连续”的。

方法四：考虑向量x[0..n]，假设sum存放了数组中x[s..i-1]这i-s个元素的和，那么temp←sum+x[i]与x[i]进行比较将存在两种情况：①若sum<0，则temp<x[i]，②若sum>0，则temp>x[i]，而x[i+1..n]向量中元素的和必然是一个定值，设为fixval，在情况①中temp+fixval<x[i]+fixval，而在情况②中则有temp+fixval>x[i]+fixval，这说明如果当temp<x[i]时，我们可以完全舍弃前i个元素组成的连续子向量，从某种意义上而言，这构成了当前最大向量和值的下界。我们接着分析，考虑已经被舍弃的向量x[s..i-1]，该子向量中必然存在一个上界k使得x[s..k]中的所有元素的和值（设为maxval）是向量x[s..i-1]中最大的，只是将该值与后续元素累加之后无法再大于maxval从而更新它，因此这相当于当前最大向量和值的上界。有了当前最大向量和值的上界和下界，那么是否就相当于得出了当前已扫描的所有元素中最大子向量的和值及其边界？从某种程度上，这是可以的，但需要通过精巧的构造。考虑maxval存放的是第一个当前向量中最大子向量的和值，如果在第二个子向量开始处，我们所得出的子向量的和值不断与maxval进行比较，我们会得出两种结果，即要么更新，要么不更新。若更新，则说明第二个向量中的子向量的和值（但不一定最大）大于第一个向量中的最大子向量。那么我们就需要更新相应的边界，更准确的说是下界，而上界则仍由maxval在当前向量中是否继续更新决定。从而：

由于只有一个循环，那么时间复杂度T(n)显然为O(n)。接下来所要做的工作就是对以上介绍的四种方法的时间复杂度进行严格证明，测试用例如下：

运行所得M文件如下：

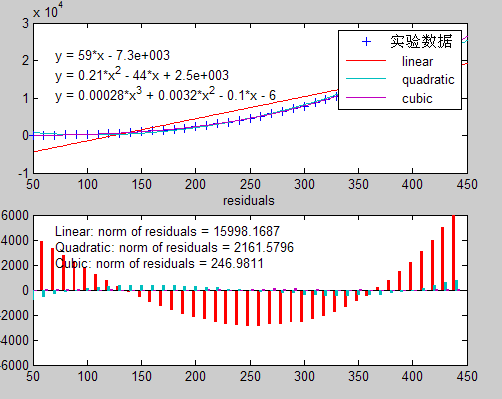
（图一：方法一执行所得图示）

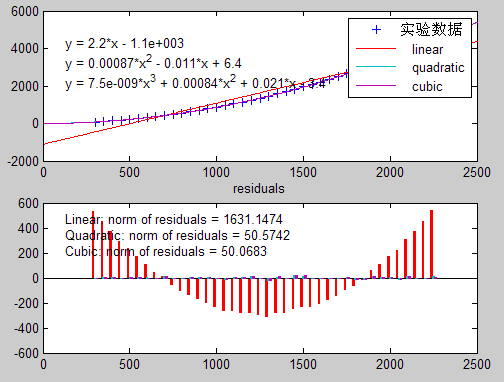
（图二：方法二执行所得图示）

（图三：方法三执行所得图示）

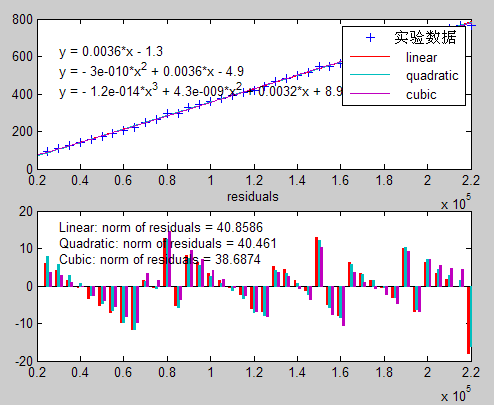
（图四：方法四执行所得图示）

由图一可以看出，若对算法一继续进行四次拟合，那么其最高次项的系数将趋于负数，因此其渐进趋于规模n的立方，与我们所得出的渐进紧确上界非常吻合。算法二同理。值得注意的是算法三，当规模较小时O(lgn)≈O(1)，因此在图三中我们看到的是该算法的运行时间复杂度为O(n)，但若对它继续进行拟合，其残差值(residuals)变化较大，说明拟合程度不高，而当其渐进趋于n的平方时，它的系数又小于0，因此我们有较大的把握可以认为他的运行时间复杂度介于O(n)~O(n2)之间，即O(nlgn)。算法四由图四所示，运行时间复杂度为O(n)没有什么问题，残差值(residuals)的较小变化也说明线性拟合已经较为精确。

小故事（纯属引用）：著名计算机科学家Andrew Appel曾写过一篇名为"An efficient program for many-body simulations"的论文，论文中探讨了当n=10000时的两个天体物理学问题，该程序解决了重力场中多个物体相互作用的经典"n体问题"，给定物体的质量、初始位置和速度，该程序对三维空间中n个物体的运行进行仿真。想象一下，这些物体可以是行星、恒星或是星系。(通过研究仿真运行，物理学家可以测试理论与天文观测的吻合程度，更多细节参见Pfalzner和Gibbon的Many-Body Tree Methods in Physics一书。)Appel估算出当n=10000时，该算法在他的计算机上运行大约需要一年的时间。(旁注：当然不是他真的运行了一年，就像上文所用的方法，研究在较小规模下运行时间与问题规模的函数关系，那么只需扩大规模，即可有较大把握推测当规模n达到10000时所需运行时间为多少。)Appel最终的程序在不到一天的时间内就解决了该问题。Appel通过几个不同层面的改进来获得巨大的加速，以下是他的真实事迹的再现：

• 算法和数据结构。Appel首先考虑选择一个高效的算法，并使用二叉树的叶子节点代表物体。结果是这一改进使得程序的运行时间缩短为原来的十二分之一。
  
• 算法调优。他和上面的"算法和数据结构"要点似乎没有多大区别。我猜测可能是后期在原算法的基础上进行的优化，比如利用存储器结构的特点，进行循环扩展，或是对函数进行内联、使用宏等手段。这样带来的结果是其运行时间再次减半。
• 数据结构重组。这主要表现在程序运行的过程中再次对原确定的数据结构进行改变以适应程序中状态的变化。结果是运行时间减半。
• 代码调优。代码调优和算法调优本质上是在同一阶段进行的。主要是由于树数据结构提供了额外的数值精度。64位双精度浮点数可以用32位单精度浮点代替，运行时间再次减半。
  
• 汇编重写。Appel对程序的性能进行监视，98%的运行时间都花在一个函数上，使用汇编重写该函数，运行速度提升为原先的2.5倍。（非常不错的优化考虑，不过不满足软件工程的要求，所以这一点在实际项目中慎用！）
• 硬件。Appel在解决该问题时是在上世纪80年代的老古董上面运行的。在上述改进之后，程序在25万美元的部门机器上运行，装配有加速器，运行时间再次减半。
  

由以上几点，最终的程序的加速为12×2×2×2×2.5×2=480。实际在项目过程中参考以上几点是非常具有现实意义的。