语音与语言处理笔记——9.语音识别

语音识别系统结构语音识别中HMM的应用特征提取：MFCCcomputing acounstic likelihoods计算声学似然度字典和语言模型search and decoding搜索解码embedded trainingevaluation评估：WER，SER...

qq_14962179

625人浏览 · 2019-01-14 20:49:41

qq_14962179 · 2019-01-14 20:49:41 发布

语音识别系统结构
noisy channel model 噪声通道模型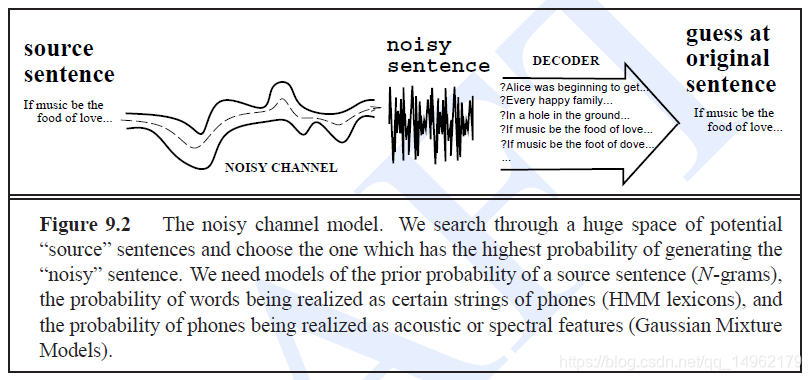

$W^=arg⁡max⁡wP(W∣O)=arg⁡max⁡wP(O∣W)P(W)P(O)=arg⁡max⁡wP(O∣W)P(W)\hat{W}=\mathop {\arg \max }\limits_w P(W|O) = \mathop {\arg \max }\limits_w \frac{{P(O|W)P(W)}}{{P(O)}} = \mathop {\arg \max }\limits_w P(O|W)P(W)$
$W^=arg⁡max⁡WP(O∣W)⏞likelyhoodθP(W)⏞prior\hat{W}=\mathop {\arg \max }\limits_W \overbrace {P(O|W)}^{likelyhood}\theta \overbrace {P(W)}^{prior}$
LM表示所给字符串作为语音源句的可能性，可由N-gram语法求的。
N-gram计算一个句子的概率：
$P(w1n)=∏k=1nP(wk∣wk−N+1k−1)P(w_1^n) = \prod\limits_{k = 1}^n {P({w_k}|w_{k - N + 1}^{k - 1})}$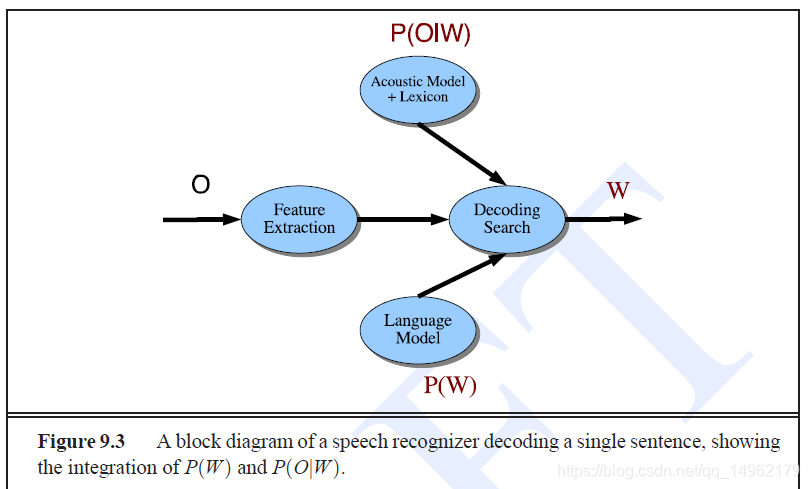

通过剪枝、快速匹配、树形词典构建来加速解码。
语音识别中HMM的应用

HMM组成：

$Q=q_1q_2q...q_N$ 一系列状态集
A 转移概率矩阵
O 观察序列，每个O对应一个词序列V
B 观察似然度，也叫做发射概率，是观察序列 $o_t$ 由状态i产生的概率
$q_0,q_end$ 初始状态和结束状态，与观察序列无关
Viterbi算法用于HMM解码，Baum_Welch/Forward-Backward算法用于训练HMMs。
在语音识别中，隐含状态是音素、子音素或字词；观察序列是某一时刻波形的能量或频谱；解码就是将声学信息和字词序列相匹配。
声学特征矢量：一般是每10ms为一帧，1s中包含100帧，每一帧用一个长度为39的实值特征来表示频谱信息。
对于小词汇语音识别，可以以word直接建模，比如数字识别，yes_no识别。对于大词汇量语音识别，可以用音素建模，中文识别可用声韵母进行建模。
以音素状态建模six:a basic phone HMM for the word six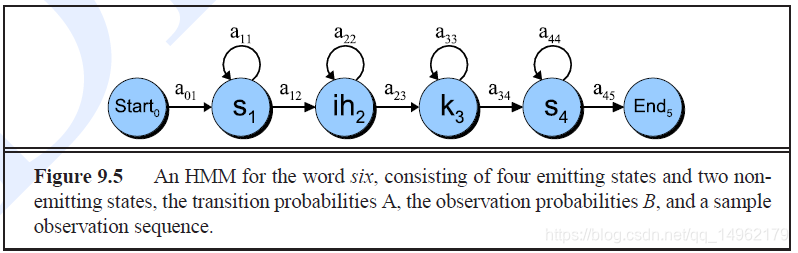

在语音识别hmm中，状态只能进行自转移或连续转移，不能进行随意转移。
Bakis network：left-to-right HMM结构，只有左右状态转移和self-loops。
一般情况下一帧为10ms，一个音素持续时间一般为20ms，但有时候有些音素甚至持续1s，也就是100帧的数据。
在LVASR中，通常使用3个HMM状态对一个因素建模，分别表示开始状态，中间状态，结束状态。用3个emitting状态和2个non_emittting状态(为初始状态和结束状态)如图9.7。静音一般采用5个状态进行建模。
通常对word model或phone model 5状态建模，采用word HMM状态。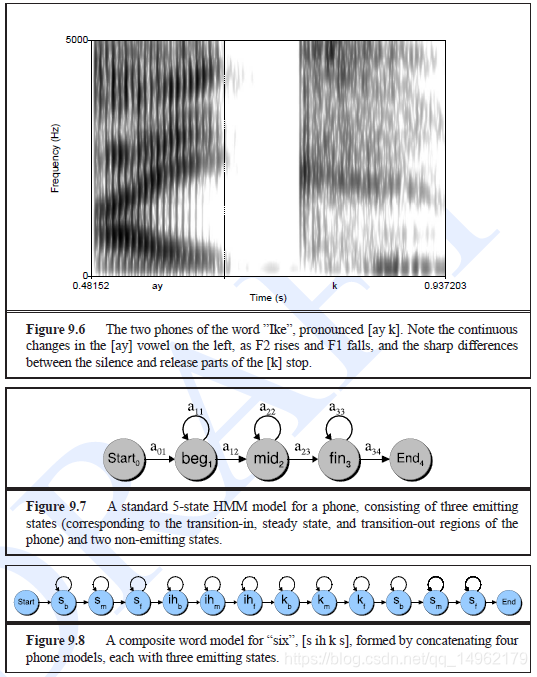

语音识别的HMM模型参数化为：
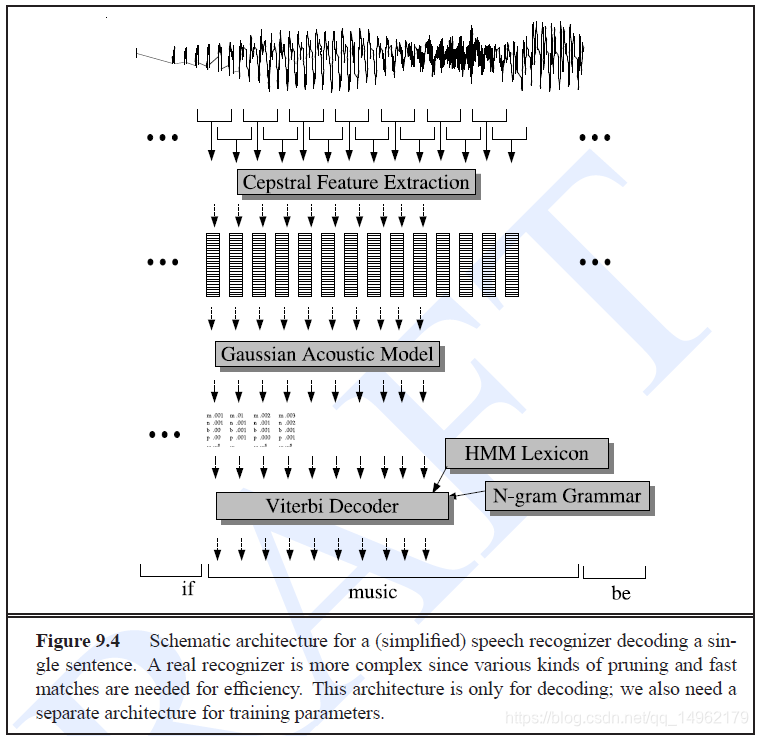
特征提取：MFCC
AD模数转换两个步骤：采样和量化。
采样率一般为8kHz或16kHz。
奈奎斯特采样定理：采样率应该大于等于信号最大频率的2倍，才能DA数模转换无损恢复原始信号。
在人类语言中，大多数语音信号的频率低于10kHz。
量化：8位(-128~127),16位(-32768——32767)
MFCC特征提取步骤：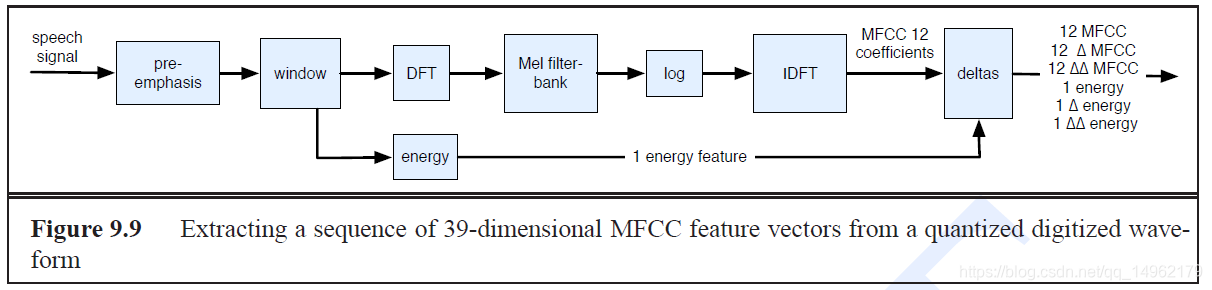

a.Preemphasis预加重
b.Windowing加窗
c.DFT(离散傅里叶变换)
d.Mel filter bank and log梅尔滤波器组和取对数
e.
computing acounstic likelihoods计算声学似然度
a.vector quantization矢量量化
b.Guassian PDFs 高斯概率密度函数
Univariate Guassians一维高斯
用高斯概率密度函数作为一位声学矢量的观察似然度函数。
用Guassian pdf计算似然度 $b_j(o_t)$
$bj(ot)=12πσj2exp⁡(−(x−μj)22σj2){b_j}({o_t}) = \frac{1}{{\sqrt {2\pi {\sigma _j}^2} }}\exp ( - \frac{{{{(x - {\mu _j})}^2}}}{{2{\sigma _j}^2}})$
训练时计算均值和方差：
$μ^i=1T∑t=1Tot s.t. qt is state i{{\hat \mu }_i} = \frac{1}{T}\sum\limits_{t = 1}^T {{o_t}\ s.t.\ {q_t}}\ is\ state\ i$
$σ^j2=1T∑t=‘T(ot−μi)2 s.t. qt is state i\hat \sigma _j^2 = \frac{1}{T}\sum\limits_{t = `}^T {({o_t}} - {\mu _i}{)^2}\ s.t.\ {q_t}\ is\ state\ i$
用Baum_Welch算法更新后的 $μ^\hat \mu$ 和 $σ^2\hat \sigma^2$ :
$μ^i=∑t=1Nξt(i)ot∑t=1Nξt(i){{\hat \mu }_i} = \frac{{\sum\limits_{t = 1}^N {{\xi _t}(i){o_t}} }}{{\sum\limits_{t = 1}^N {{\xi _t}(i)} }}$
$σ^j2=∑t=1Nξt(i)(ot−μi)2∑t=1Nξt(i)\hat \sigma _j^2 = \frac{{\sum\limits_{t = 1}^N {{\xi _t}(i){{({o_t} - {\mu _i})}^2}} }}{{\sum\limits_{t = 1}^N {{\xi _t}(i)} }}$
multivariate Gaussians 多元高斯
pdf：
$f(x⃗∣μ⃗,Σ)=1(2π)D2∣Σ∣12exp⁡(−12(x−μ)TΣ−1(x−μ))f(\vec x|\vec \mu ,\Sigma ) = \frac{1}{{{{(2\pi )}^{\frac{D}{2}}}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}\exp ( - \frac{1}{2}{(x - \mu )^T}{\Sigma ^{ - 1}}(x - \mu ))$
协方差矩阵 $Σ\Sigma$ 表示每一维的方差和任意两维之间的协方差。
两个随机变量X和Y之间的协方差为：
$Σ=E[(X−E(X)(Y−E(Y)]=∑i=1Np(XiYi)(Xi−E(X))(Yi−E(Y))\Sigma = E[(X - E(X)(Y - E(Y)] = \sum\limits_{i = 1}^N {p({X_i}{Y_i})} ({X_i} - E(X))({Y_i} - E(Y))$
多元高斯观察概率估计为：
$bj(ot)=1(2π)D2∣Σ∣12exp⁡(−12(ot−μj)TΣj−1(ot−μj)){b_j}({o_t}) = \frac{1}{{{{(2\pi )}^{\frac{D}{2}}}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}\exp ( - \frac{1}{2}{({o_t} - {\mu _j})^T}{\Sigma _j}^{ - 1}({o_t} - {\mu _j}))$

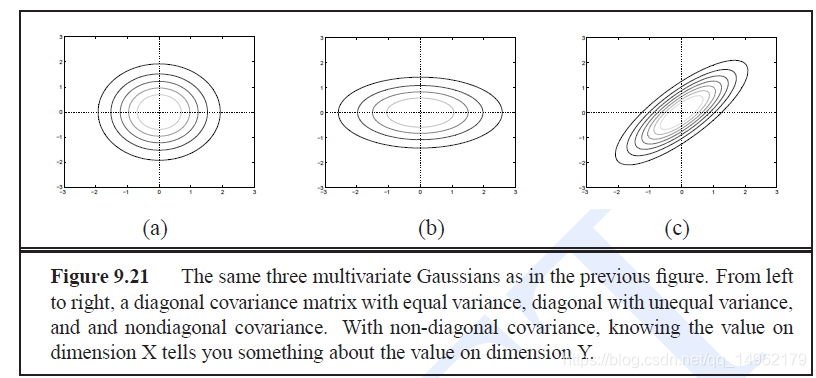
对角协方差矩阵多元高斯：[{({o_t} - {\mu _i})^T}]
$bj(ot)=∏d=1D12πσjd2exp⁡(−12[(otd−μjd)2σjd2]){b_j}({o_t}) = \prod\limits_{d = 1}^D {\frac{1}{{\sqrt {2\pi \sigma _{jd}^2} }}} \exp ( - \frac{1}{2}[\frac{{{{({o_{td}} - {\mu _{jd}})}^2}}}{{\sigma _{jd}^2}}])$
用Baum_Welch算法更新后的 $μ^\hat \mu$ 和 $σ^2\hat \sigma^2$ :
$μ^i=∑t=1Tξt(i)ot∑t=1Tξt(i){{\hat \mu }_i} = \frac{{\sum\nolimits_{t = 1}^T {{\xi _t}(i){o_t}} }}{{\sum\nolimits_{t = 1}^T {{\xi _t}(i)} }}$
$σ^i2=∑t=1Tξt(i)(ot−μi)(ot−μi)T∑t=1Tξt(i)\hat \sigma _i^2 = \frac{{\sum\nolimits_{t = 1}^T {{\xi _t}(i){{({o_t} - {\mu _i})}}{({o_t} - {\mu _i})^T}} }}{{\sum\nolimits_{t = 1}^T {{\xi _t}(i)} }}$
Gaussian Mixture Models高斯混合模型
GMM PDF：
$f(x∣μ,Σ)=∑k=1Mck12π∣Σk∣exp⁡((x−μk)TΣ−1(x−μk))f(x|\mu ,\Sigma ) = \sum\limits_{k = 1}^M {{c_k}\frac{1}{{\sqrt {2\pi \left| {{\Sigma _k}} \right|} }}} \exp ({(x - {\mu _k})^T}{\Sigma ^{ - 1}}(x - {\mu _k}))$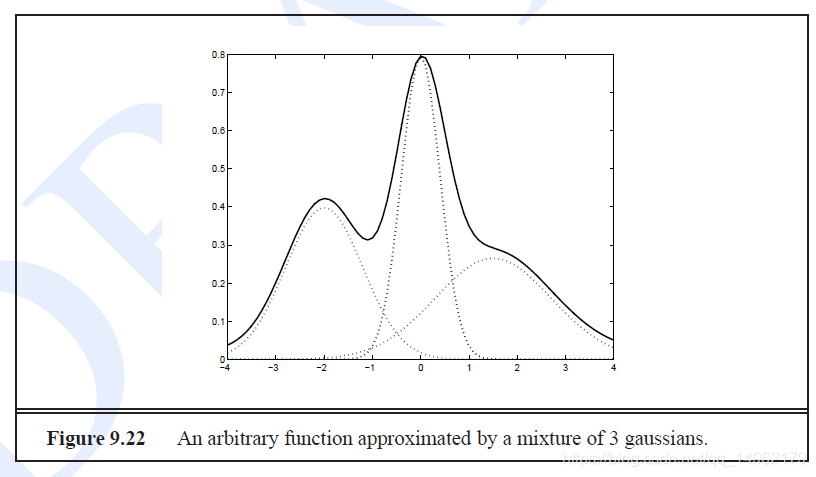

$bj(ot)=∑m=1Mcjm12π∣Σjm∣exp⁡[(ot−μjm)TΣjm−1(ot−μjm)]{b_j}({o_t}) = \sum\limits_{m = 1}^M {{c_{jm}}\frac{1}{{\sqrt {2\pi \left| {{\Sigma _{jm}}} \right|} }}} \exp [{({o_t} - {\mu _{jm}})^T}{\Sigma _{jm}}^{ - 1}({o_t} - {\mu _{jm}})]$
$ξtm(j)\xi_{tm}(j)$ mean the probability of being in state j at time t with mth mixture component accounting for the output observation $o_t$
$ξtm(j)=∑i=1Nαt−1(j)aijcjmbjm(ot)βt(j)αT(F){\xi _{tm}}(j) = \frac{{\sum\nolimits_{i = 1}^N {{\alpha _{t - 1}}(j){a_{ij}}{c_{jm}}{b_{jm}}({o_t}){\beta _t}(j)} }}{{{\alpha _T}(F)}}$
c.probilities,log probilities and distance functions
(1)数值下溢，概率值都非常小，因此语音识别中通常使用对数概率。
(2)加速计算，概率连乘取对数后可变为相加。
字典和语言模型
search and decoding搜索解码
解码问题可描述为：给定一系列声学观察序列，我们应该如何选择具有最高后验概率的单词序列。
使用贝叶斯规则，最优单词序列是最大化语言模型先验概率和声学模型似然度乘积的概率。
贝叶斯公式得到最优字词序列：
$W^=arg⁡max⁡WP(O∣W)⏞likelyhoodP(W)⏞prior\hat W = \mathop {\arg \max }\limits_W \overbrace {P(O|W)}^{likelyhood}\overbrace {P(W)}^{prior}$
加入语言模型分数，language model scaling factor LMSF，大于1(对于许多系统在5-15之间)，用于降低语言模型概率值。
$W^=arg⁡max⁡WP(O∣W)P(W)LMSF\hat W = \mathop {\arg \max }\limits_W P(O|W)P{(W)^{LMSF}}$
word insertion penalty WIP:字插入补偿，加入WIP之后公式为
$W^=arg⁡max⁡WP(O∣W)P(W)LMSFWIPN\hat W = \mathop {\arg \max }\limits_W P(O|W)P{(W)^{LMSF}}WIP^N$
WIP是一个常数，N是文字长度。
取对数概率后，解码公式为：
$W^=arg⁡max⁡Wlog⁡P(O∣W)+LMSF×log⁡P(W)+N×log⁡WIP\hat W = \mathop {\arg \max }\limits_W \log P(O|W) + LMSF \times \log P(W){\rm{ + }}N \times \log WIP$
语音识别HMM模型参数：

每个单词的HMM结构来自发音词典。一般使用现成的字典，每个音素由3个子音素组成，两个转移部分，是自环和转下下一子音素(转移概率分别为0.5)。在每个字的结束部分有一个静音音素来将字分隔开。
A和B矩阵在嵌入式训练(embeded training)过程中由Baum-Welch算法训练得到。

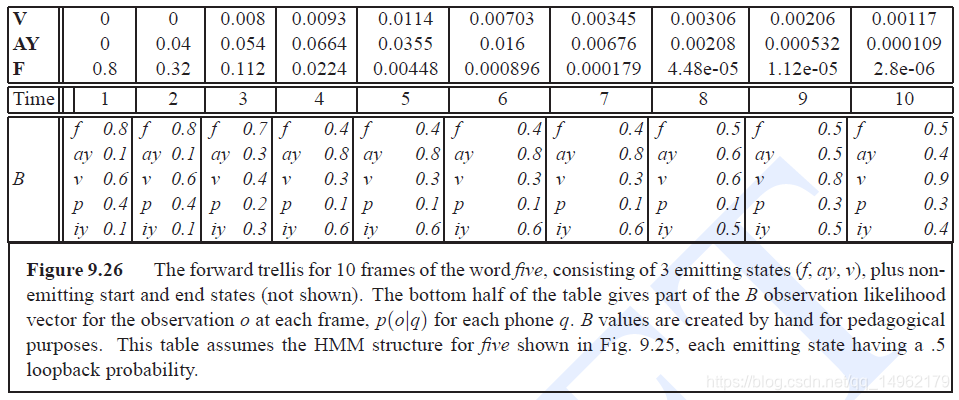
在这里插入图片描述
用前向算法和维特比算法进行解码：
前向算法计算观察序列似然度，
$αt(j)\alpha_t(j)$ 前向概率，表示看到前t个观察值，第t个状态为j的概率。
$αt(j)=P(o1,o2...ot,qt=j∣λ)\alpha_t(j)=P(o_1,o_2...o_t,q_t=j|\lambda)$
$αt(j)=∑i=1Nαt−1aijbj(ot)\alpha_t(j)=\sum\limits_{i=1}^N\alpha_{t-1}a_{ij}b_j(o_t)$
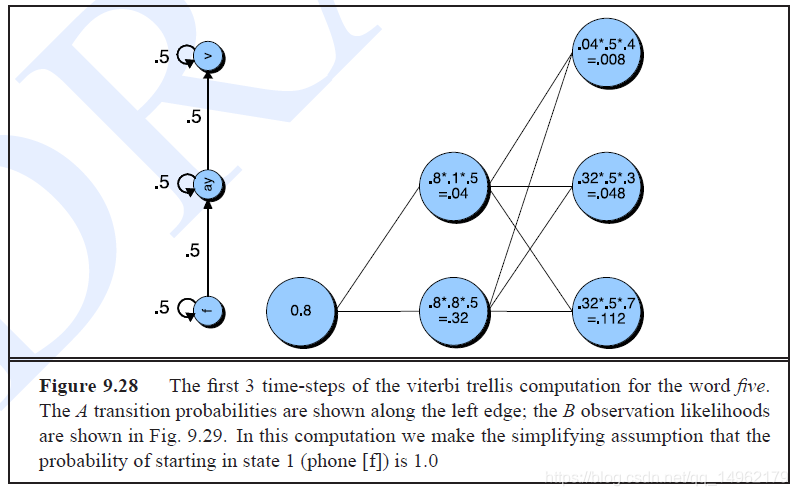
在这里插入图片描述

Viterbi算法返回最有可能的状态序列。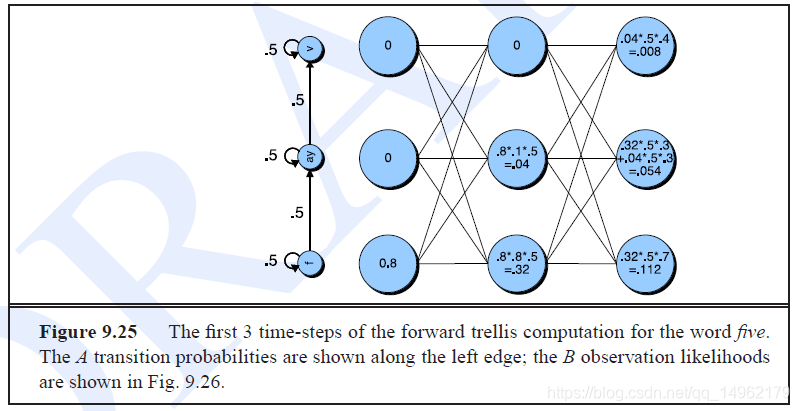

在Viterbi算法中， $v_t(j)$ 表示看到前t个观察值并且最有可能状态序列为 $q_1q_2...q{t-1}时第t个状态为j的概率$
$vt(j)=P(q0,q1...qt−1,o1,o2...ot,qt=j∣λ)v_t(j)=P(q_0,q_1...q_{t-1},o_1,o_2...o_t,q_t=j|\lambda)$
$vt(j)=max⁡i=1Nvt−1(i)aijbj(ot)v_t(j)=\max\limits_{i=1}^Nv_{t-1}(i)a_{ij}b_j(o_t)$
在这里插入图片描述
viterbi算法与前向算法类似，只不过前向算法时求和，而viterbi算法时求最大值。

跨字解码需要加入语言模型，一般用N-Gram.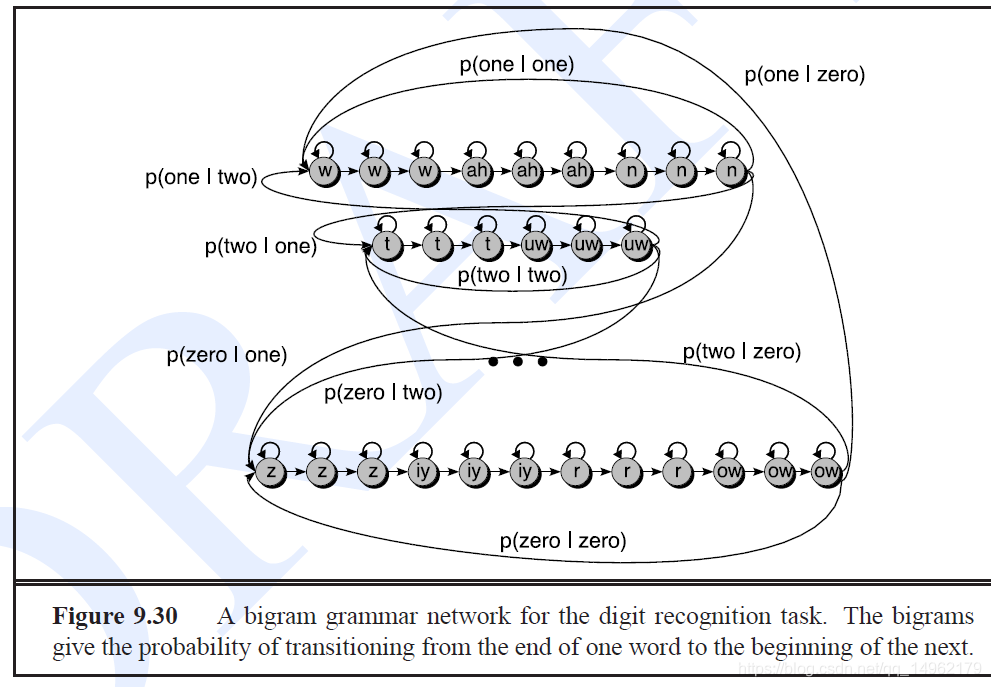

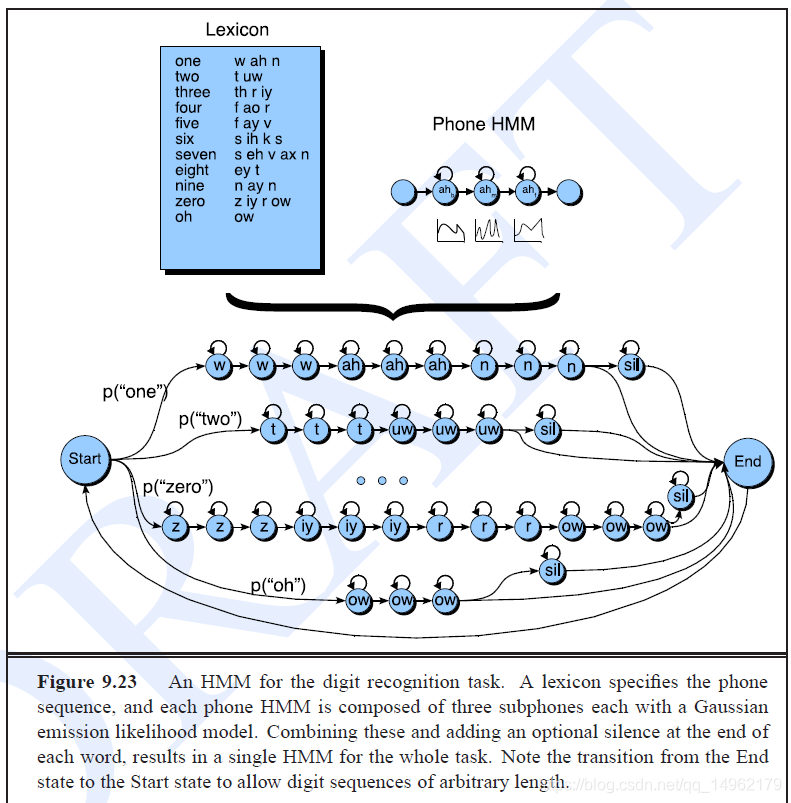
用于数字识别任务的二元语法语言网络。二元语法给出从一个单词的结尾到下一个单词的开头的过渡概率。
多字解码任务的HMM网格的示意图：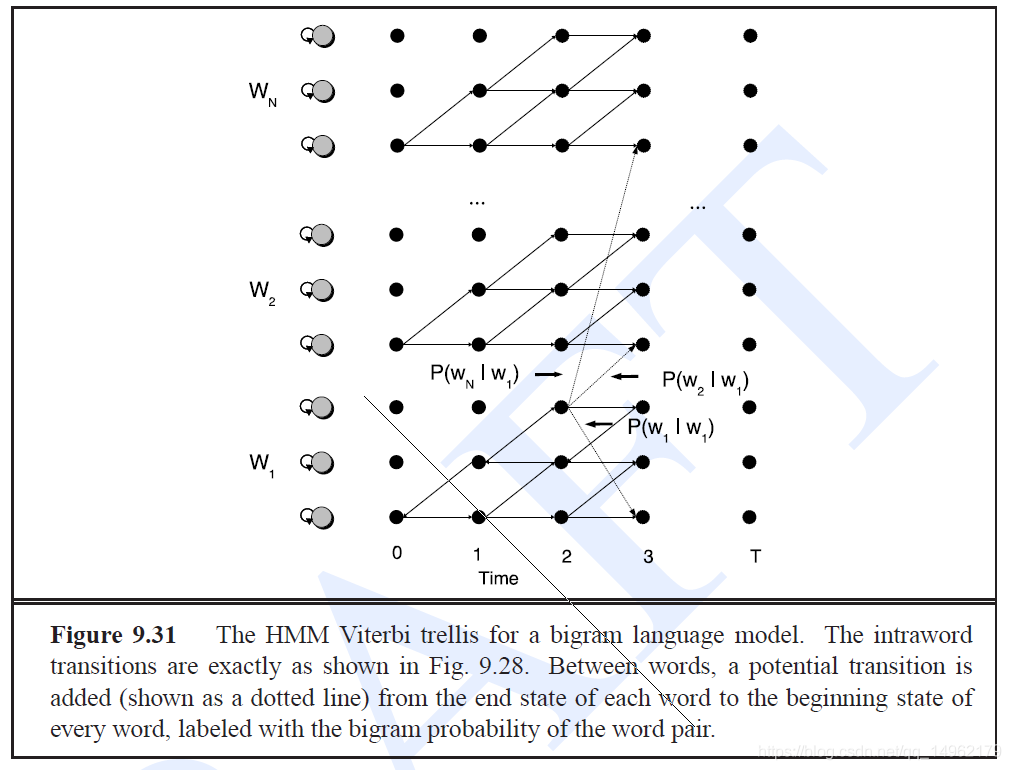
在这里插入图片描述
字内转移概率由A矩阵得到，字间转移概率由语言模型得到。
一旦整个维特比网格计算出话语，我们就可以从最后时间步的最可能状态开始，然后向后跟踪回溯指针以获得最可能的状态序列，从而得到最可能的字符串。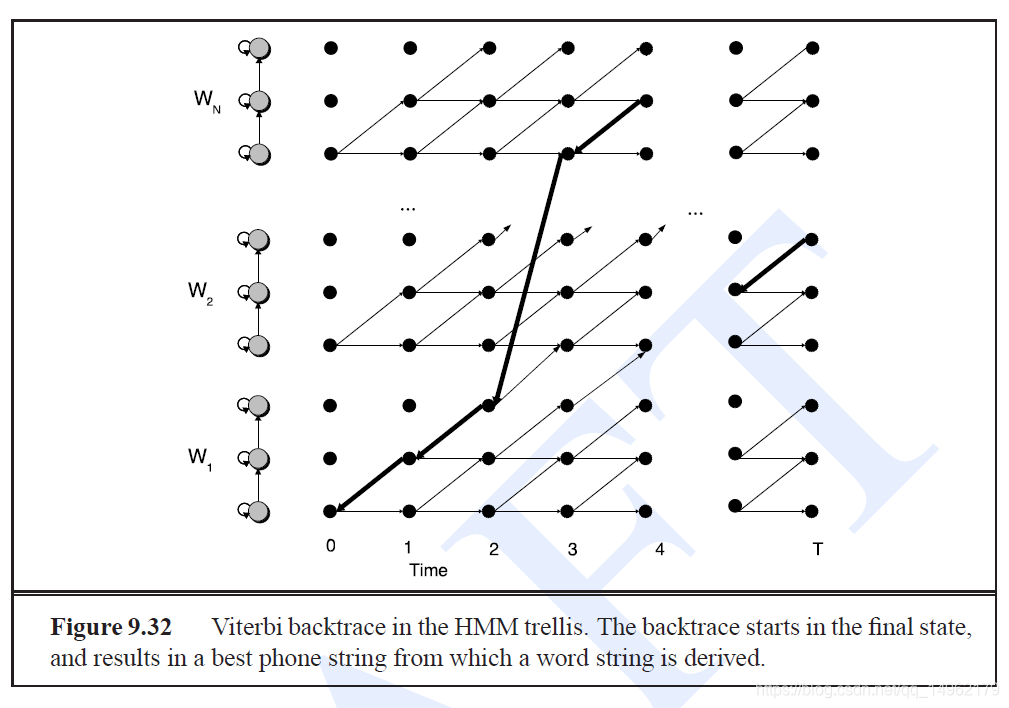
在这里插入图片描述
Pruning剪枝：用于加速解码。在大词汇量识别的实践中，我们并不考虑所有算法将路径从一个状态列扩展到下一个状态列时可能的单词。相反，每次PRUNING步骤都会修剪低概率路径，而不会扩展到下一个状态列。
7. embedded training
在这里插入图片描述
8. evaluation评估：WER，SER