牛客网专题训练 算法岗
深度学习考虑某个具体问题时,你可能只有少量数据来解决这个问题。不过幸运的是你有一个类似问题已经预先训练好的神经网络。可以用下面哪种方法来利用这个预先训练好的网络?(样本少,相似性低)–> 冻结训练(样本多,相似性低)–> 重新训练(样本少,相似性高)–> 修改输出层(样本多,相似性高)–> 预训练权+重新训练样本少,相似性低 --> 冻结训练样本多,相似性低 --&g
NLP
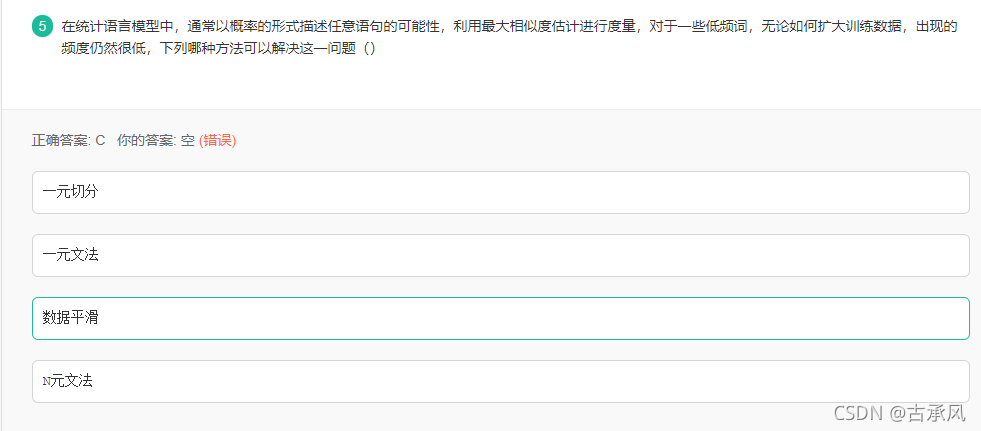
在估计概率时,容易想到的方法是使用频率估计概率,然而由于训练集不可能出现所有可能的序列,因此可能有很多序列的概率估计为0,但这些未出现的序列不代表着不会出现,为了解决这个问题,将这些未出现的序列赋予一个极小的不为零的概率值作为估计,这种方式就是数据平滑。
深度学习
考虑某个具体问题时,你可能只有少量数据来解决这个问题。不过幸运的是你有一个类似问题已经预先训练好的神经网络。可以用下面哪种方法来利用这个预先训练好的网络?
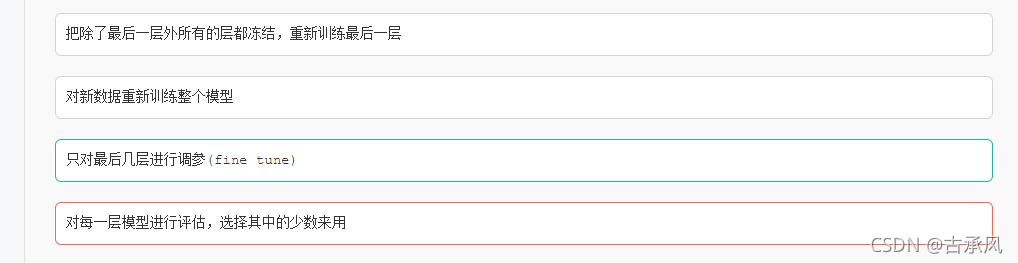
(样本少,相似性低)–> 冻结训练
(样本多,相似性低)–> 重新训练
(样本少,相似性高)–> 修改输出层
(样本多,相似性高)–> 预训练权+重新训练
样本少,相似性低 --> 冻结训练
样本多,相似性低 --> 重新训练
样本少,相似性高 --> 修改输出层
样本多,相似性高 --> 预训练权重+重新训练
CNN
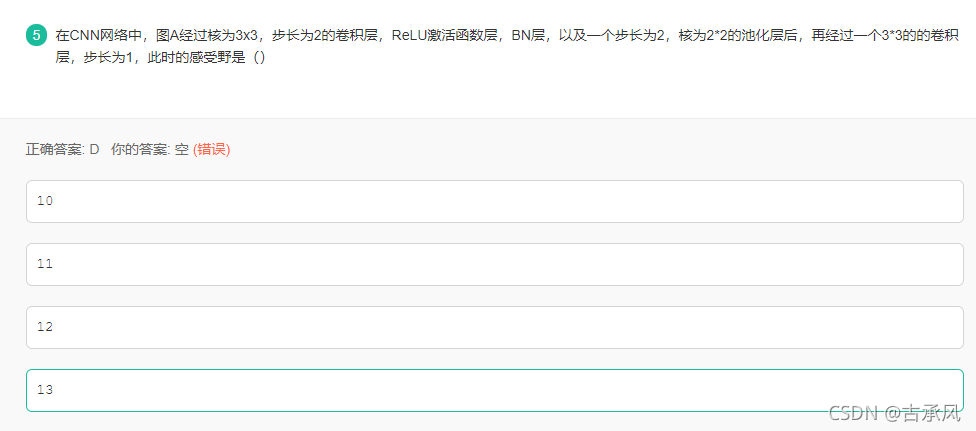
RFi−1=(RFi−1)∗stridei−1+ksizei−1 RF_{i-1} =(RF_i-1)*stride_{i-1} + ksize_{i-1} RFi−1=(RFi−1)∗stridei−1+ksizei−1
数理统计
假设在今日头条里面,有很多工作人员检查新闻是不是属于虚假新闻,所有新闻真实率到达了98%,工作人员在检验一个真实的新闻把它检验为一个虚假的新闻的概率为2%,而一个虚假的新闻被检验为真实的新闻的概率为5%.那么,一个被检验为真实的新闻确实是真实的新闻的概率是多大?
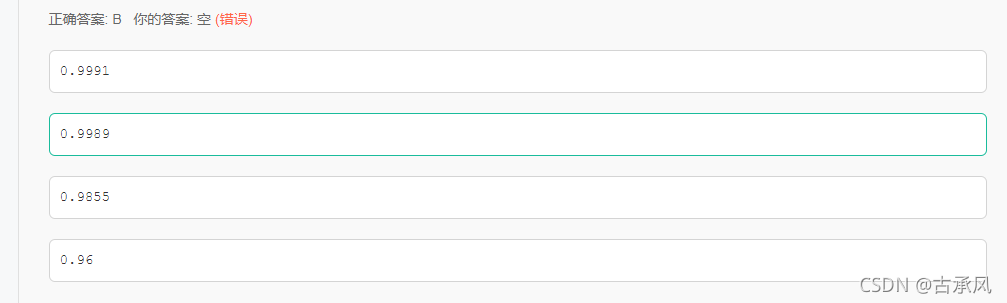
假设总共100个新闻,那么真实新闻为98个,虚假新闻为2个,检验为真实的新闻 总个数为真实的检验为真实的 和虚假的检验为真实的 之和:98x(1-2%)+2x5%=96.14个,其中检验为真实的真实新闻个数即是真实的检验为真实的 个数:98x(1-2%)=96.04个,所以其真实概率为96.04/96.14=0.9989…
H同学每天乘公交上学,早上睡过头或遇到堵车都会迟到;H早上睡过头的概率为0.2,路上遇到堵车的概率为0.5;若某天早上H迟到了,那么以下推测正确的有()。
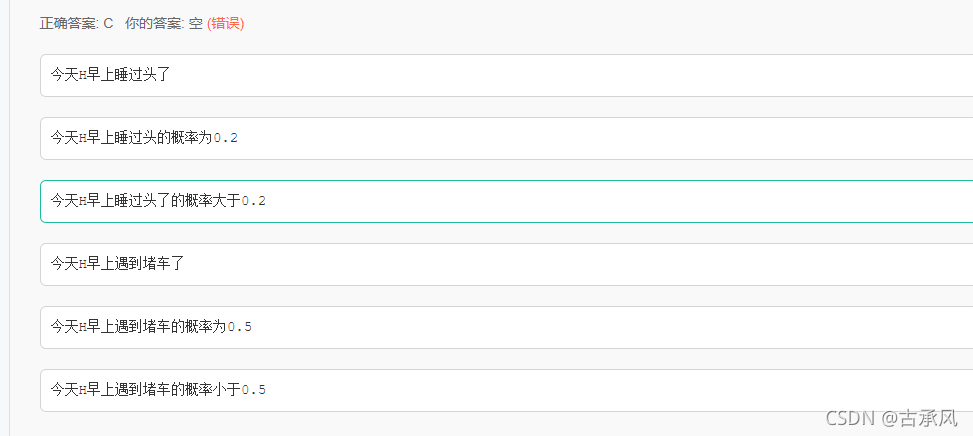
H没迟到概率(1-0.2) * (1-0.5) = 0.4
H迟到概率0.6
P(H睡过头|H迟到)=P(H睡过头H迟到)/P(H迟到) = 0.2 / 0.6 = 1/3
P(路上遇到堵车|H迟到)=P(路上遇到堵车H迟到)/P(H迟到) = 0.5 / 0.6 = 5/6
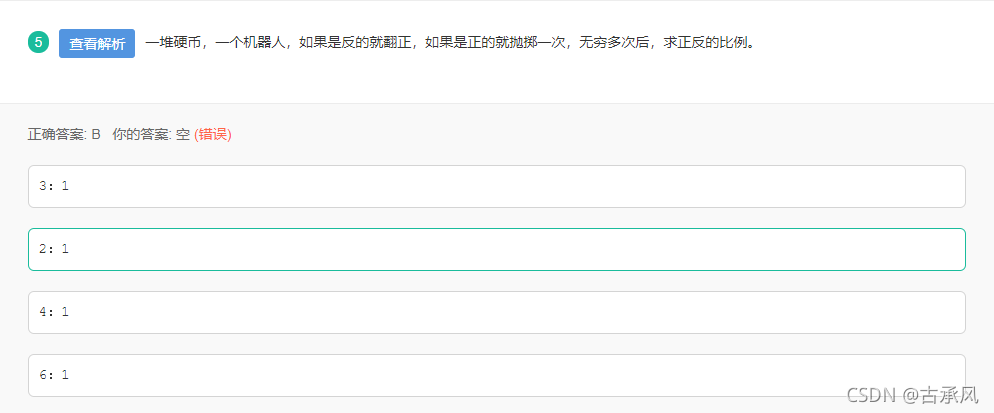
这个问题关键有2点: 1.状态转移条件,如果为反就翻正,如果是正就抛掷一次 2.状态终止条件,本次翻转后得到的正反比例,和下次翻转后得到的正反比例相同 设某个阶段正面的比例为p,则反面的比例为1-p。下一次执行转移条件,正面的比例为p/2 + (1-p),反面的比例为p/2,根据终止条件得到方程: p / (1-p) = (p/2 + (1-p)) / (p/2) ==> p = 2 / 3; 本次正面 :本次反面 == 下次正面 :下次反面 因此正反比例为 p / (1-p) = 2 : 1
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)