二叉搜索树是一颗二叉树且满足性质：设x是二叉树的一个节点。如果y是x左子树的一个节点，那么y.key 小于等于 x.key；如果y是x右子树的一个节点，那么y.key大于等于 x.key

二叉搜索树的操作： 查询 插入 删除

左边小
右边大

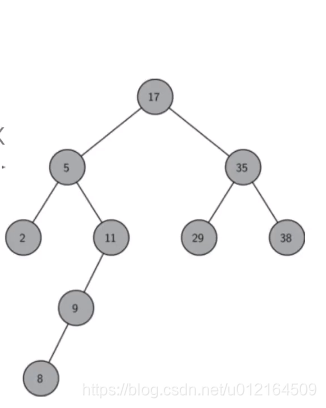
从右往左读

#! /usr/bin/env python
# -*- coding: utf-8 -*-

import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None   # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None

class BST:
    def __init__(self, li=None):
        #创建要给根节点 
        self.root = None
        #不是none
        if li:
            for val in li:
                self.insert_no_rec(val)

    #插入 node是节点   val是值  递归
    def insert(self, node, val):
        #node是空
        if not node:
            #只是创建节点，但是没有连接起来  空树，递归不需要特殊出来
            node = BiTreeNode(val)
        #12 < 17 往左走
        elif val < node.data:
            #这是父亲连着左孩子   --这是左孩子
            node.lchild = self.insert(node.lchild, val)
            #这是左孩子的父亲是 --这是父亲
            node.lchild.parent = node
            #这是右孩子
        elif val > node.data:
            node.rchild = self.insert(node.rchild, val)
            #右孩子连着父亲
            node.rchild.parent = node
        return node

    #非递归 
    def insert_no_rec(self, val):
        #根节点
        p = self.root
        #没值
        if not p:               # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            #左子树
            if val < p.data:
                if p.lchild:
                    #左子树有 p=左子树,往左子树走一下,继续往下走
                    p = p.lchild
                else:           # 左孩子不存在  左子树是个none没有,我就把它插入就可以了   这是父找子   --这是孩子 
                    p.lchild = BiTreeNode(val)
                    #子找父亲，练级父亲   --这是父亲
                    p.lchild.parent = p
                    return
            #右子树
            elif val > p.data:
            	#有值,
                if p.rchild:
                	#父亲链接右孩子
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    #查询递归
    def query(self, node, val):
        #如果是空数
        if not node:
            return None
        #右边找  值大于数是往右边找
        if node.data < val:
            return self.query(node.rchild, val)
        #左边找
        elif node.data > val:
            return self.query(node.lchild, val)
        else:
            return node

    #非递归 是没有node。直接p就循环了
    def query_no_rec(self, val):
        #根节点 
        p = self.root
        while p:
            if p.data < val:
                p = p.rchild
            elif p.data > val:
                p = p.lchild
            else:
                return p

        #p是空 找不到,返回None
        return None


    #前序 根左右
    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    #中序 左根右
    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    #后序 左右根
    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')

li = list(range(0,500,2))
random.shuffle(li)
#查询 查10
tree = BST(li)
print(tree.query_no_rec(10).data)
#
#插入
#li = list(range(100))
#tree = BST(li)
#tree.pre_order(tree.root)
#print("")
#tree.in_order(tree.root)
#print("")
#tree.post_order(tree.root)
#print("")
#删除
# tree.delete(4)
# tree.delete(1)
# tree.delete(8)
# tree.in_order(tree.root)

#插入的

#查询

1、如果要删除的节点是叶子节点： 直接删除

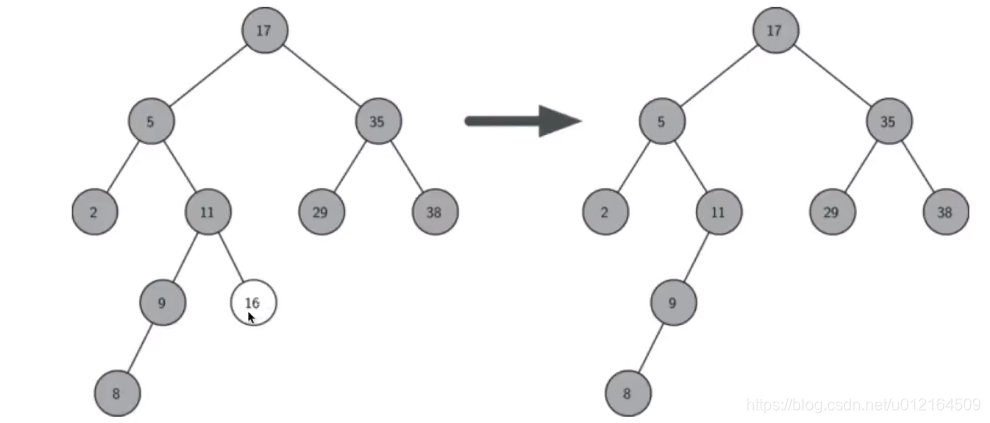
如果要删除的节点只有一个孩子： 将此节点的父亲与孩子连接然后删除该节点

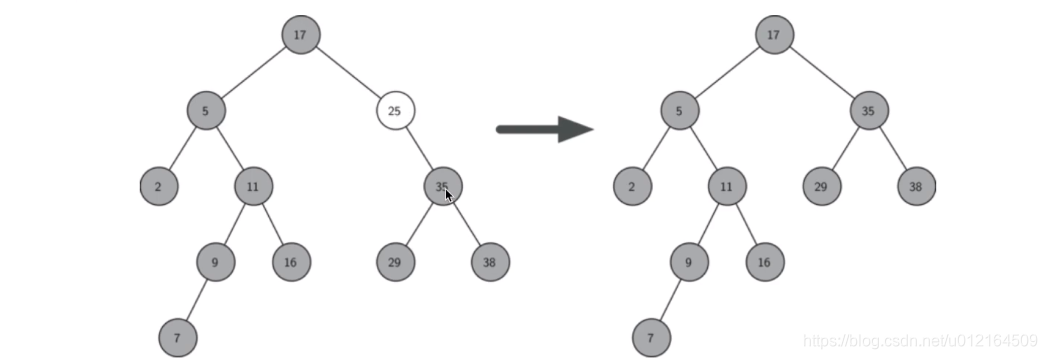
如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多有一个右孩子）删除，并替换当前节点

删5就要删7 图7

往左走，走的最小，是7，8都不行，不能往右走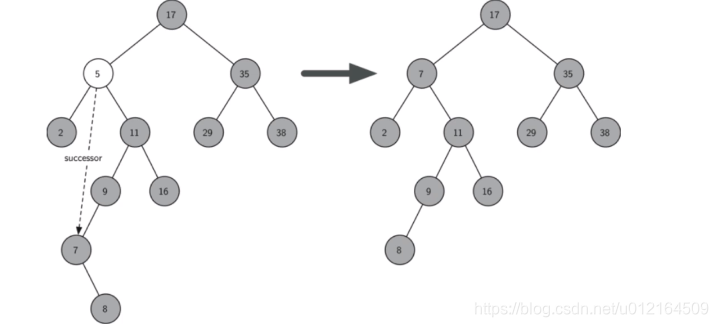

#! /usr/bin/env python
# -*- coding: utf-8 -*-

import random

class BiTreeNode:
        def __init__(self, data):
                self.data = data
                self.lchild = None   # 左孩子
                self.rchild = None  # 右孩子
                self.parent = None


class BST:
        def __init__(self, li=None):
                #创建要给根节点 
                self.root = None
                #不是none
                if li:
                        for val in li:
                                self.insert_no_rec(val)

        #插入 node是节点   val是值
        def insert(self, node, val):
        #node是空
                if not node:
                #只是创建节点，但是没有连接起来  空树，递归不需要特殊出来
                        node = BiTreeNode(val)
                #12 < 17 往左走
                elif val < node.data:
                #这是父亲连着孩子   --这是孩子
                        node.lchild = self.insert(self.lchild, val)
                #这是孩子连着父亲 --这是父亲
                        node.lchild.parent = node
                elif val > node.data:
                        node.rchild = self.insert(self.rchild, val)
                        node.rchild.parent = node
                return node

        #非递归 
        def insert_no_rec(self, val):
                #根节点
                p = self.root
                if not p:               # 空树
                        self.root = BiTreeNode(val)
                        print(self.root)
                        return
                while True:
                #左子树
                        if val < p.data:
                                print(p)
                                if p.lchild:
                                        #左子树有 p=左子树,往左子树走一下,继续往下走
                                        p = p.lchild
                                else:           # 左孩子不存在  左子树是个none没有,我就把它插入就可以了   这是父找子   --这是孩子 
                                        p.lchild = BiTreeNode(val)
                                        #子找父亲   --这是父亲
                                        p.lchild.parent = p
                                        return
                                        #右子树
                        elif val > p.data:
                                if p.rchild:
                                        p = p.rchild
                                else:
                                        p.rchild = BiTreeNode(val)
                                        p.rchild.parent = p
                                        return
                        else:
                                return


        #查询
        def query(self, node, val):
                #如果是空
                if not node:
                        return None
                #右边找
                if node.data < val:
                        return self.query(node.rchild, val)
                #左边找
                elif node.data > val:
                        return self.query(node.lchild, val)
                else:
                        return node

        #非递归
        def query_no_rec(self, val):
                #根节点 
                p = self.root
                while p:
                        if p.data < val:
                                p = p.rchild
                        elif p.data > val:
                                p = p.lchild
                        else:
                                return p
                        #返回None
                return None


        #前序
        def pre_order(self, root):
                if root:
                        print(root.data, end=',')
                        self.pre_order(root.lchild)
                        self.pre_order(root.rchild)

        #中序
        def in_order(self, root):
                if root:
                        self.in_order(root.lchild)
                        print(root.data, end=',')
                        self.in_order(root.rchild)

        #后序
        def post_order(self, root):
                if root:
                        self.post_order(root.lchild)
                        self.post_order(root.rchild)
                        print(root.data, end=',')

        def __remove_node_1(self, node):
        # 情况1：node是叶子节点
                if not node.parent:   #树就这一个节点，你要把它删除了 根节点 
                        self.root = None  #变成空树
                #node是它父亲的左孩子  如果这个值是父亲的左孩子
                if node == node.parent.lchild:  #node是它父亲的左孩子  node.parent是父亲  就把它的孩子变为None
                        node.parent.lchild = None
                        #node.parent =None
                else:   #右孩子
                        node.parent.rchild = None

		#node.lchild自己定义的
        #只有一个左孩子
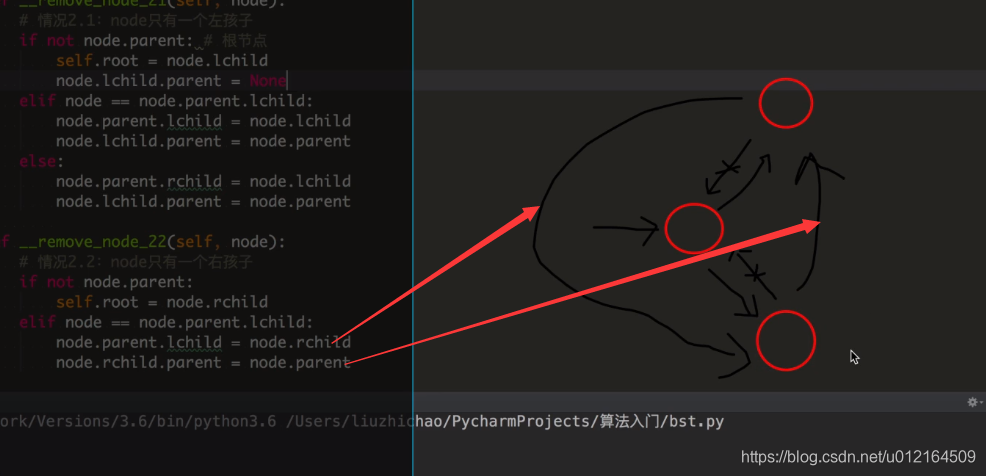
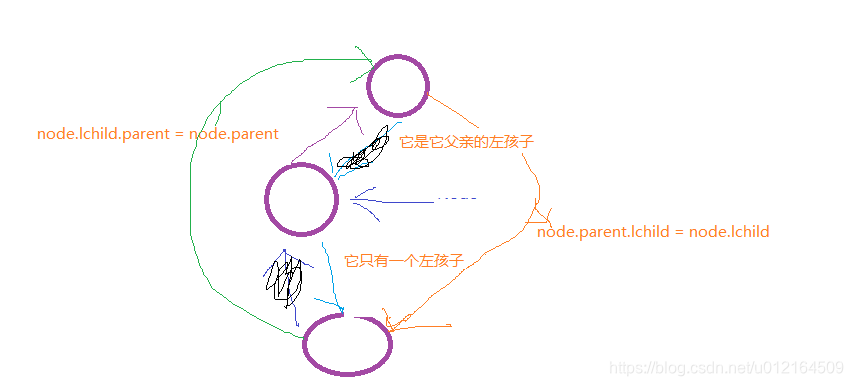
        def __remove_node_21(self, node):
                # 情况2.1：node只有一个左孩子
                if not node.parent: # #判断是否为根节点，没有根节点
                        self.root = node.lchild  #如果没有根节点，它的左孩子继承了根节点,就是新的根
                        node.lchild.parent = None
                        #node的值是
                elif node == node.parent.lchild:
                        #父亲和孩子连接起来
                        #node.parent父亲
                        #node.lchild传的值的左孩子
                        #通过lchild 连接起来
                        node.parent.lchild = node.lchild  #它的node.parent父亲,跟他左孩子node.lchild连接起来 
                        #孩子连接它的父亲
                        node.lchild.parent = node.parent
                else:
                        #父亲根它的孩子(只有左孩子)，通过右孩子连接
                        node.parent.rchild = node.lchild
                        #左孩子根它父亲
                        node.lchild.parent = node.parent

        #只有一个右孩子 
        def __remove_node_22(self, node):
                # 情况2.2：node只有一个右孩子
                if not node.parent:
                        self.root = node.rchild
                elif node == node.parent.lchild:
                        node.parent.lchild = node.rchild
                        node.rchild.parent = node.parent
                else:
                        node.parent.rchild = node.rchild
                        node.rchild.parent = node.parent

        def delete(self, val):
                if self.root:   # 不是空树
                        node = self.query_no_rec(val)
                        if not node: # 不存在
                                return False
                        if not node.lchild and not node.rchild: #1. 叶子节点 没有左孩子和没有右孩子
                                self.__remove_node_1(node)
                        elif not node.rchild:       # 2.1 只有一个左孩子 右孩子没有
                                self.__remove_node_21(node)
                        elif not node.lchild:       # 2.2 只有一个右孩子 左孩子没有
                                self.__remove_node_22(node)
                        else:   # 3. 两个孩子都有  右孩子最小值   删除5 min_node是11  
                                min_node = node.rchild
                                #11的左孩子
                                while min_node.lchild:
                                		#找到了7
                                        min_node = min_node.lchild
                                #先把数据放过来   把最小的节点7替换到5呢 看图7
                                node.data = min_node.data
                                        # 删除min_node  删除再看是满足min_node的1还是2
                                if min_node.rchild:
                                       self.__remove_node_22(min_node)
                                else:
                                       self.__remove_node_1(min_node)


#li = list(range(0,500,2))
#random.shuffle(li)

#tree = BST(li)
#print(tree.query_no_rec(10).data)
#
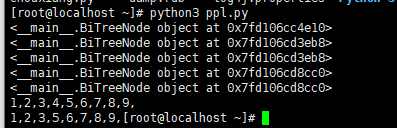
tree = BST([1,4,2,5,3,8,6,9,7])
#tree = BST(li)

tree.in_order(tree.root)
print("")
#tree.in_order(tree.root)
#print("")
#tree.post_order(tree.root)
#print("")
tree.delete(4)
# tree.delete(1)
# tree.delete(8)
tree.in_order(tree.root)

平均情况下，二叉搜索树进行搜索的时间 复杂度为O(lgn)

最坏情况下，二叉搜索树可能非常偏斜

解决方案

• 随机化插入
• AVL树