akaze特征匹配怎么去掉不合适的点_基于opencv的轮廓匹配算法:python代码实现
写在前⾯模式识别领域有⼀个经典问题:边缘轮廓提取。轮廓提取是很多算法的基础,例如霍夫直线检测、霍夫圆检测、snake主动轮廓模型等。在轮廓提取后,为了加快算法的效率,通常会对轮廓进⾏过滤,去掉不需要的噪声轮廓,这⼀步往往使⽤的⽅法就是轮廓匹配。轮廓匹配算法的强⼤远远不⽌于此,在图像纹理信息较简单的情况下,可以使⽤轮廓匹配算法直接找到⽬标,进⾏精确的定位。如图,如何在右图中精准地找到左图的四⻆星?本
写在前⾯
模式识别领域有⼀个经典问题:边缘轮廓提取。轮廓提取是很多算法的基础,例如霍夫直线检测、霍夫圆检测、snake主动轮廓模型等。在轮廓提取后,为了加快算法的效率,通常会对轮廓进⾏过滤,去掉不需要的噪声轮廓,这⼀步往往使⽤的⽅法就是轮廓匹配。轮廓匹配算法的强⼤远远不⽌于此,在图像纹理信息较简单的情况下,可以使⽤轮廓匹配算法直接找到⽬标,进⾏精确的定位。如图,如何在右图中精准地找到左图的四⻆星?本⽂将教⼤家如何使⽤轮廓匹配算法来解决这个问题。

轮廓匹配原理
轮廓匹配的原理是利⽤轮廓的不变性特征来判断轮廓之间的相似度,模式识别领域的⼀位先贤Hu.M.K在1962年找到了这些特征,并证明了他们具有旋转,缩放和平移不变性。这些特征也以这位先贤的名字命名,它们统称为Hu矩。Hu矩包括下⾯7个矩,这个是经过⼆阶和三阶规格中⼼矩推导出来的。图像Hu矩的物理意义:
- 0阶矩(m00):目标区域的质量
- 1阶矩(m01,m10):目标区域的质心
- 2阶矩(m02,m11,m20):目标区域的旋转半径
- 3阶矩(m03,m12,m21,m30):目标区域的方位和斜度,反应目标的扭曲
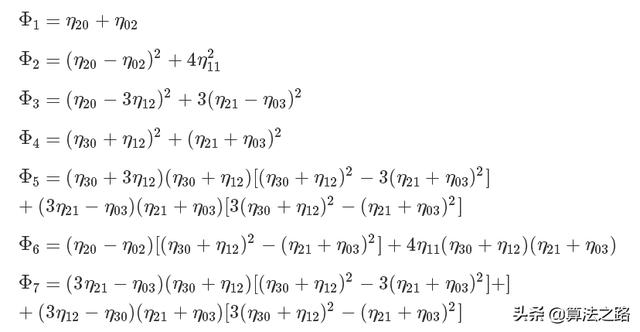
Hu矩的7个公式
图像Hu矩的python计算代码如下,如果理解了Hu矩的意义,其实并不复杂,Hu矩的计算对象是一个点集,可以是一个轮廓,也可以是一个灰度图。这里以灰度图为例:
def humoments(img_gray): ''' 由于7个不变矩的变化范围很大,为了便于比较,可利用取对数的方法进行数据压缩;同时考虑到不变矩有可能出现负值的情况,因此,在取对数之前先取绝对值 经修正后的不变矩特征具有平移 、旋转和比例不变性 ''' # 标准矩定义为m_pq = sumsum(x^p * y^q * f(x, y)) row, col = img_gray.shape #计算图像的0阶几何矩 m00 = img_gray.sum() m10 = m01 = 0 # 计算图像的二阶、三阶几何矩 m11 = m20 = m02 = m12 = m21 = m30 = m03 = 0 for i in range(row): m10 += (i * img_gray[i]).sum() m20 += (i ** 2 * img_gray[i]).sum() m30 += (i ** 3 * img_gray[i]).sum() for j in range(col): m11 += i * j * img_gray[i][j] m12 += i * j ** 2 * img_gray[i][j] m21 += i ** 2 * j * img_gray[i][j] for j in range(col): m01 += (j * img_gray[:, j]).sum() m02 += (j ** 2 * img_gray[:, j]).sum() m30 += (j ** 3 * img_gray[:, j]).sum() # 由标准矩我们可以得到图像的"重心" u10 = m10 / m00 u01 = m01 / m00 # 计算图像的二阶中心矩、三阶中心矩 y00 = m00 y10 = y01 = 0 y11 = m11 - u01 * m10 y20 = m20 - u10 * m10 y02 = m02 - u01 * m01 y30 = m30 - 3 * u10 * m20 + 2 * u10 ** 2 * m10 y12 = m12 - 2 * u01 * m11 - u10 * m02 + 2 * u01 ** 2 * m10 y21 = m21 - 2 * u10 * m11 - u01 * m20 + 2 * u10 ** 2 * m01 y03 = m03 - 3 * u01 * m02 + 2 * u01 ** 2 * m01 # 计算图像的归格化中心矩 n20 = y20 / m00 ** 2 n02 = y02 / m00 ** 2 n11 = y11 / m00 ** 2 n30 = y30 / m00 ** 2.5 n03 = y03 / m00 ** 2.5 n12 = y12 / m00 ** 2.5 n21 = y21 / m00 ** 2.5 # 计算图像的七个不变矩 h1 = n20 + n02 h2 = (n20 - n02) ** 2 + 4 * n11 ** 2 h3 = (n30 - 3 * n12) ** 2 + (3 * n21 - n03) ** 2 h4 = (n30 + n12) ** 2 + (n21 + n03) ** 2 h5 = (n30 - 3 * n12) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) + (3 * n21 - n03) * (n21 + n03) * (3 * (n30 + n12) ** 2 - (n21 + n03) ** 2) h6 = (n20 - n02) * ((n30 + n12) ** 2 - (n21 + n03) ** 2) + 4 * n11 * (n30 + n12) * (n21 + n03) h7 = (3 * n21 - n03) * (n30 + n12) * ((n30 + n12) ** 2 - 3 * (n21 + n03) ** 2) + (3 * n12 - n30) * (n21 + n03) * (3 * (n30 + n12) ** 2 - (n21 + n03) ** 2) inv_m7 = [h1, h2, h3, h4, h5, h6, h7] inv_m7 = np.log(np.abs(inv_m7)) return inv_m7利⽤Hu矩进⾏轮廓匹配
轮廓实质上就是⼀些轮廓点的集合,因此轮廓也可以⽤Hu矩来判断相似度,这⾥给出⼀个利⽤Hu矩形状匹配的例⼦和代码,opencv的cv2.matchShapes函数内置了Hu矩的计算⽅式,默认的匹配⽅式就是Hu矩匹配,因此这⾥就不必自己手动计算7个Hu矩啦。轮廓匹配流程⽐较简单,分两步:
- 利⽤边缘提取算法,找到模板轮廓
- 与候选轮廓⼀⼀匹配,相似度最⼤的即为⽬标轮廓
import cv2import numpy as npfrom matplotlib import pyplot as plt img1 = cv2.imread('star.jpg', 0)img2 = cv2.imread('star2.jpg', 0)ret, thresh = cv2.threshold(img1, 127, 255, 0)ret, thresh2 = cv2.threshold(img2, 127, 255, 0)contours1, hierarchy = cv2.findContours(thresh, 2, 1)cnt_star = contours1[2] # 模版轮廓contours2, hierarchy = cv2.findContours(thresh2, 2, 1)min_ret = 999 min_id = 0for i, cnt2 in enumerate(contours2): ret = cv2.matchShapes(cnt_star, cnt2, 1, 0.0) # ret越小,越相似 if ret < min_ret: min_ret = ret min_id = i print(min_id, min_ret)show_img = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)cv2.drawContours(show_img, contours2, min_id, (0, 0, 255), -1)plt.imshow(show_img)效果展示
运⾏轮廓匹配的代码,A、B、C三个轮廓的相似度分别为0.0004、0.16、0.32,因此A为相似度最高的轮廓,画出响应最⼤的轮廓区域,如图,成功找到了正确⽬标。

更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)