文章目录

零、本节目标

在这里插入图片描述

一、线性回归的基本思想

用训练样本集估计模型中的参数，使模型在最小平方误差意义下能够最好地拟合训练样本。

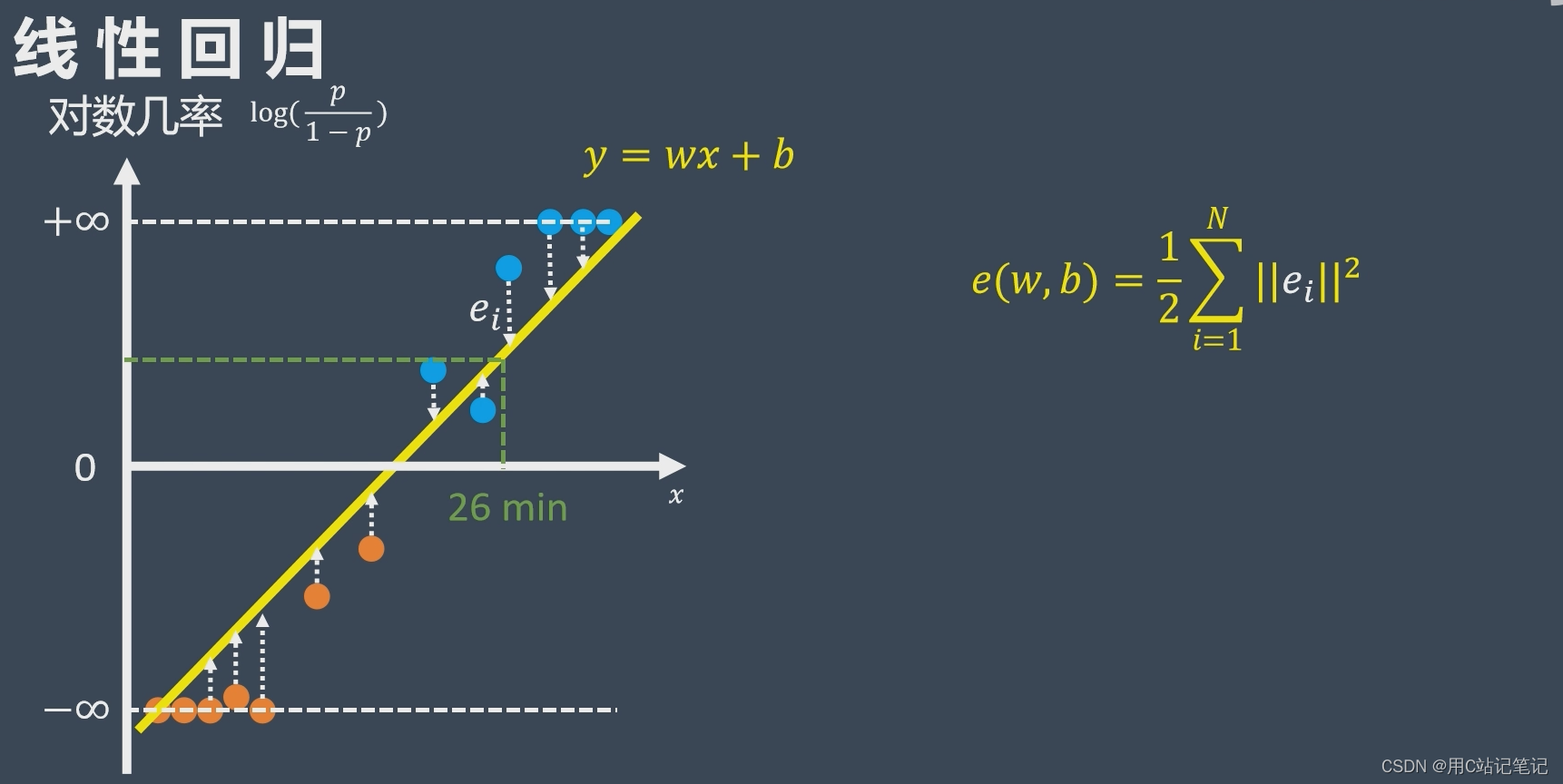
在这里插入图片描述

例题

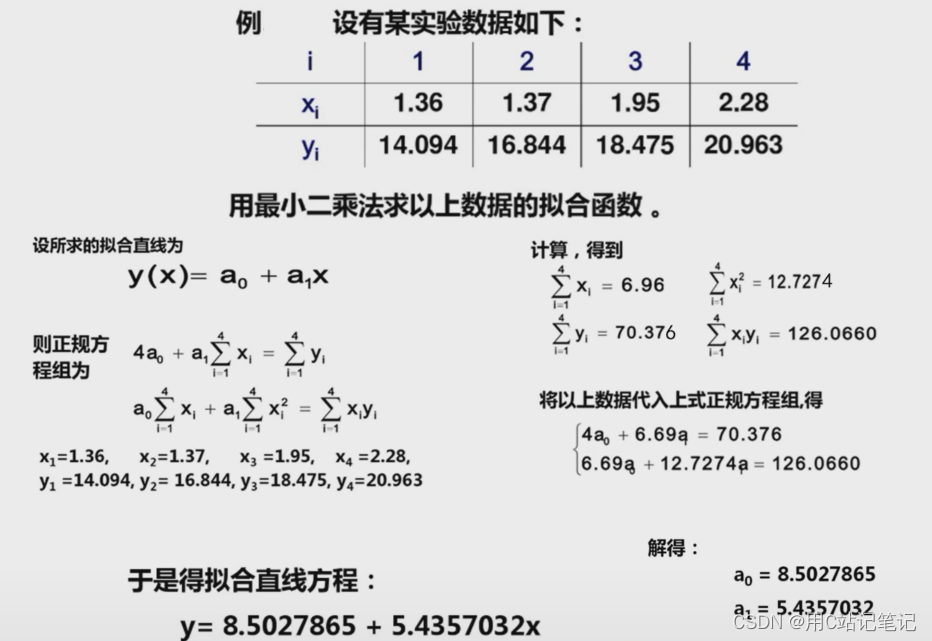
在这里插入图片描述

二、线性判别函数基本概念
表达式

在这里插入图片描述

决策规则

在这里插入图片描述方程 g(x)=0 定义了一个决策面，它把归类于ω1类的点和归类于ω2的点分隔开。当g(x)为线性函数时，这个决策面是超平面。

三、Fisher线性判别分析方法（没怎么说）
简述Fisher准则函数

在这里插入图片描述

Fisher线性判别

可以考虑把d维空间的样本投影到一条直线上，形成一维空间，即把维数压缩到一维，这在数学上容易办到。然而，即使样本在d维空间里形成若干紧凑的互相分得开的集群，如果把它们投影到一条任意的直线上，也可能使得几类样本混在一起而变得无法识别。 但是在一般情况下， 总可以找到某个方向， 使得在这个方向的直线上，样本的投影能分开得最好。问题是如何根据实际情况找到这条最好的、最易于分类的投影线，这就是Fisher算法所要解决的基本问题。

四、感知器基本原理（没怎么说）

在这里插入图片描述

梯度下降算法（老师没强调）

在这里插入图片描述

算法原理

在这里插入图片描述

  1. 定义代价函数
  2. 选择起始点
  3. 计算梯度
  4. 按学习率前进
  5. 重复第三步直至找到函数最小值
五、最优分类超平面（重点强调了模型，考了）

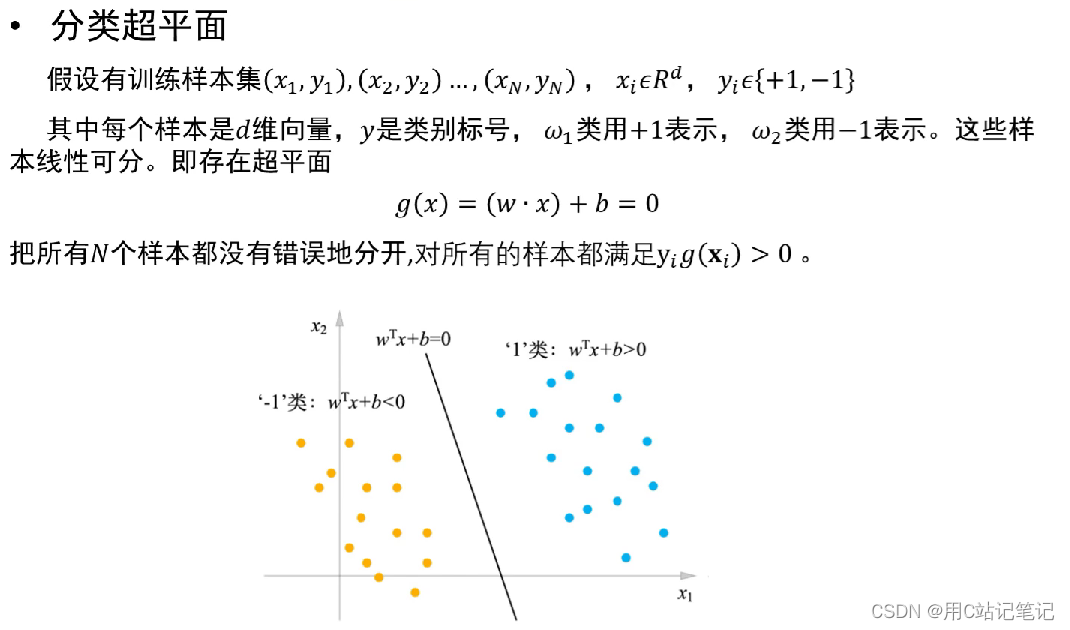
在这里插入图片描述

  1. 超平面的判断
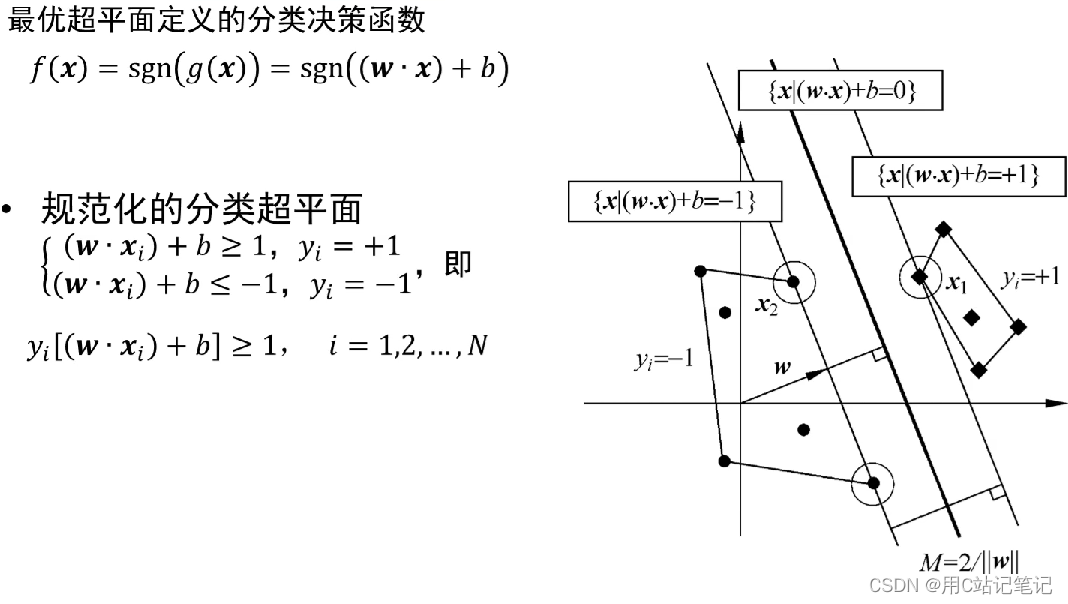
    在这里插入图片描述

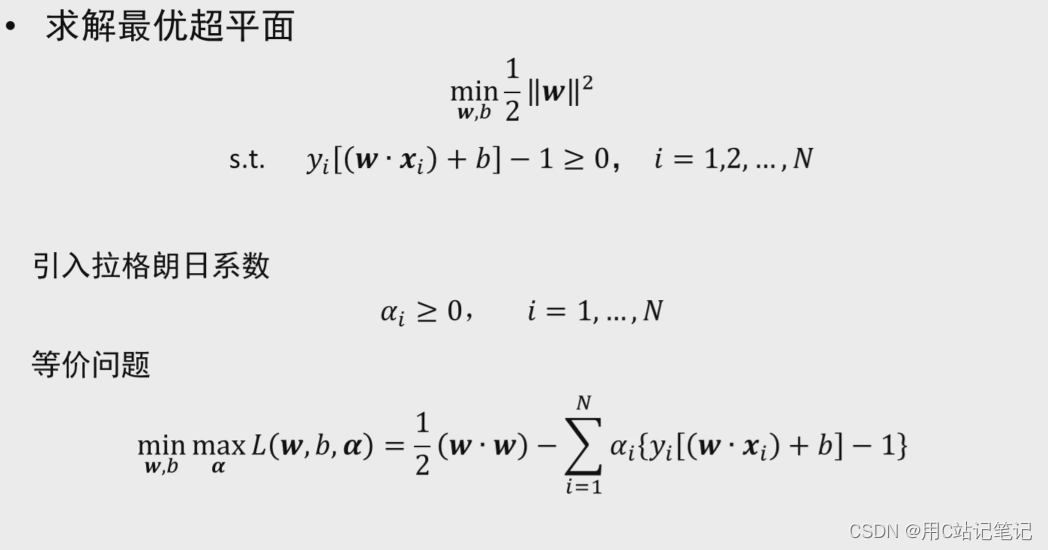
在这里插入图片描述

  1. 优化函数
    在这里插入图片描述

  2. 求解不重要

在这里插入图片描述

六、线性支持向量机（没怎么说）

在这里插入图片描述

补充：线性分类器的三种最优准则（没怎么说）

在这里插入图片描述

# 机器学习 # 算法
Logo
CSDN学习社区

CSDN联合极客时间，共同打造面向开发者的精品内容学习社区，助力成长！

更多推荐

cover

Kaldi之父，IEEE Fellow，小米首席语音科学家Daniel Povey将出席2024全球机器学习技术大会并发表演讲！

avatar CSDN学习社区
cover

探索神经网络在商品销售和图像识别中的应用

avatar CSDN学习社区
cover

基于stm32F103的座面声控台灯

avatar CSDN学习社区