聚类分析是一种重要的人类行为，早在孩提时代，一个人就通过不断改进下意识中的聚类模式来学会如何区分猫狗、动物植物。目前在许多领域都得到了广泛的研究和成功的应用，如用于模式识别、数据分析、图像处理、市场研究、客户分割、Web文档分类等[1]。

聚类就是按照某个特定标准(如距离准则)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起，不同数据尽量分离。

聚类技术[2]正在蓬勃发展，对此有贡献的研究领域包括数据挖掘、统计学、机器学习、空间数据库技术、生物学以及市场营销等。各种聚类方法也被不断提出和改进，而不同的方法适合于不同类型的数据，因此对各种聚类方法、聚类效果的比较成为值得研究的课题。

1 聚类算法的分类

目前，有大量的聚类算法[3]。而对于具体应用，聚类算法的选择取决于数据的类型、聚类的目的。如果聚类分析被用作描述或探查的工具，可以对同样的数据尝试多种算法，以发现数据可能揭示的结果。

主要的聚类算法可以划分为如下几类：划分方法、层次方法、基于密度的方法、基于网格的方法以及基于模型的方法[4-6]。

每一类中都存在着得到广泛应用的算法，例如：划分方法中的k-means[7]聚类算法、层次方法中的凝聚型层次聚类算法[8]、基于模型方法中的神经网络[9]聚类算法等。
　
目前,聚类问题的研究不仅仅局限于上述的硬聚类，即每一个数据只能被归为一类，模糊聚类[10]也是聚类分析中研究较为广泛的一个分支。模糊聚类通过隶 属函数来确定每个数据隶属于各个簇的程度，而不是将一个数据对象硬性地归类到某一簇中。目前已有很多关于模糊聚类的算法被提出，如著名的FCM算法等。

本文主要对k-means聚类算法、凝聚型层次聚类算法、神经网络聚类算法之SOM,以及模糊聚类的FCM算法通过通用测试数据集进行聚类效果的比较和分析。

2 四种常用聚类算法研究

2.1 k-means聚类算法

k-means是划分方法中较经典的聚类算法之一。由于该算法的效率高，所以在对大规模数据进行聚类时被广泛应用。目前，许多算法均围绕着该算法进行扩展和改进。

k-means算法以k为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。k-means算法的处理过程如下：首先，随机地 选择k个对象，每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇;然后重新计算每个簇的平均值。 这个过程不断重复，直到准则函数收敛。通常，采用平方误差准则，其定义如下：

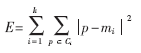
这里E是数据库中所有对象的平方误差的总和，p是空间中的点，mi是簇Ci的平均值[9]。该目标函数使生成的簇尽可能紧凑独立，使用的距离度量是欧几里得距离,当然也可以用其他距离度量。k-means聚类算法的算法流程如下：
输入：包含n个对象的数据库和簇的数目k；
输出：k个簇，使平方误差准则最小。
步骤：
　　(1) 任意选择k个对象作为初始的簇中心；
　　(2) repeat；
　　(3) 根据簇中对象的平均值，将每个对象(重新)赋予最类似的簇；
　　(4) 更新簇的平均值，即计算每个簇中对象的平均值；
　　(5) until不再发生变化。

2.2 层次聚类算法

根据层次分解的顺序是自底向上的还是自上向下的，层次聚类算法分为凝聚的层次聚类算法和分裂的层次聚类算法。

凝聚型层次聚类的策略是先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类，它们只是在簇间相似度的定义上有所不同。四种广泛采用的簇间距离度量方法如下：

这里给出采用最小距离的凝聚层次聚类算法流程：
　(1) 将每个对象看作一类，计算两两之间的最小距离；
　(2) 将距离最小的两个类合并成一个新类；
　(3) 重新计算新类与所有类之间的距离；
　(4) 重复(2)、(3)，直到所有类最后合并成一类。

2.3 SOM聚类算法

SOM神经网络[11]是由芬兰神经网络专家Kohonen教授提出的，该算法假设在输入对象中存在一些拓扑结构或顺序，可以实现从输入空间(n维)到输出平面(2维)的降维映射，其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。

SOM网络包含输入层和输出层。输入层对应一个高维的输入向量，输出层由一系列组织在2维网格上的有序节点构成，输入节点与输出节点通过权重向量连接。 学习过程中，找到与之距离最短的输出层单元，即获胜单元，对其更新。同时，将邻近区域的权值更新，使输出节点保持输入向量的拓扑特征。
　算法流程：
　(1) 网络初始化，对输出层每个节点权重赋初值；
　(2) 将输入样本中随机选取输入向量，找到与输入向量距离最小的权重向量；
　(3) 定义获胜单元，在获胜单元的邻近区域调整权重使其向输入向量靠拢；
　(4) 提供新样本、进行训练；
　(5) 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类结果。

2.4 FCM聚类算法

1965年美国加州大学柏克莱分校的扎德教授第一次提出了‘集合’的概念。经过十多年的发展，模糊集合理论渐渐被应用到各个实际应用方面。为克服非此即彼的分类缺点，出现了以模糊集合论为数学基础的聚类分析。用模糊数学的方法进行聚类分析，就是模糊聚类分析[12]。
　　
FCM算法是一种以隶属度来确定每个数据点属于某个聚类程度的算法。该聚类算法是传统硬聚类算法的一种改进。

算法流程：
　(1) 标准化数据矩阵；
　(2) 建立模糊相似矩阵，初始化隶属矩阵；
　(3) 算法开始迭代，直到目标函数收敛到极小值；
　(4) 根据迭代结果，由最后的隶属矩阵确定数据所属的类，显示最后的聚类结果。

参考文献
[1] HAN Jia Wei， KAMBER M.数据挖掘概念与技术[M]．范明，孟晓峰，译．北京：机械工业出版社，2001．
[2] 杨小兵．聚类分析中若干关键技术的研究[D]． 杭州：浙江大学，2005．
[3] XU Rui, Donald Wunsch 1 1． survey of clustering algorithm[J]．IEEE．Transactions on Neural Networks, 2005,16(3)：645-67 8.
[4] YI Hong, SAM K． Learning assignment order of instances for the constrained k-means clustering algorithm[J]．IEEE Transactions on Systems, Man, and Cybernetics, Part B：Cybernetics,2009,39 (2)：568-574.
[5] 贺玲，吴玲达，蔡益朝．数据挖掘中的聚类算法综述[J]．计算机应用研究，2007，24(1):10-13．
[6] 孙吉贵，刘杰，赵连宇．聚类算法研究[J]．软件学报，2008，19(1)：48-61．
[7] 孔英会，苑津莎，张铁峰,等．基于数据流管理技术的配变负荷分类方法研究．中国国际供电会议，CICED2006．
[8] 马晓艳，唐雁．层次聚类算法研究[J]．计算机科学,2008,34(7)：34-36．
[9] 汪海波，张海臣，段雪丽．基于MATLAB的自组织竞争神经网络聚类研究[J]．邢台职业技术学院学报，2005，22(1)：45-47．
[10] 吕晓燕，罗立民，李祥生．FCM算法的改进及仿真实验研究[J]．计算机工程与应用，2009，45(20)：144-147．
[11] 李戈，邵峰晶，朱本浩．基于神经网络聚类的研究[J]．青岛大学学报，2001，16(4)：21-24．
[12] 戈国华,肖海波,张敏．基于FCM的数据聚类分析及matlab实现[J].福建电脑，2007，4:89-90．
[13] FISHER R A． Iris Plants Database//http：//www.ics.uci.edu/~mlearn /MLRepository．Html．Authorized license．

转自：http://www.cnblogs.com/William_Fire/archive/2013/02/09/2909499.html