---

前言

  卷积神经网络（CNN）是一种深度学习模型，广泛应用于图像处理、语音识别、自然语言处理等领域。

• 图像分类和识别：CNN在图像分类和识别方面的应用是最为广泛的。通过训练，CNN能够学习到从图像中提取特征的能力，从而实现对图像的分类和识别。例如，在人脸识别、物体检测、车牌识别等领域，CNN都取得了显著的效果。
• 语音识别：CNN也可以应用于语音识别领域，通过对语音信号的卷积和池化处理，提取出语音的特征表示，从而实现对语音的分类和识别。
• 自然语言处理：CNN在自然语言处理领域也有广泛应用，例如文本分类、情感分析、命名实体识别等。通过将文本转换为特征向量，CNN能够学习到文本的特征表示，从而实现对文本的分类和识别。
• 自动驾驶：CNN在自动驾驶领域的应用主要是通过对图像的处理和分析，实现对车辆和行人的检测和跟踪，从而辅助自动驾驶系统进行决策和控制。
• 机器人视觉：CNN在机器人视觉领域的应用主要是通过对图像的处理和分析，实现机器人的导航、避障等功能。
• 超分辨率图像重建：CNN可以用于超分辨率图像重建，通过对低分辨率图像的处理和分析，重建出高分辨率图像。
• 视频分析：CNN在视频分析领域的应用主要是通过对视频的处理和分析，实现视频分类、目标检测、行为识别等功能。
• 金融领域：CNN在金融领域的应用主要是通过对金融数据的处理和分析，实现股票预测、风险管理等功能。

---

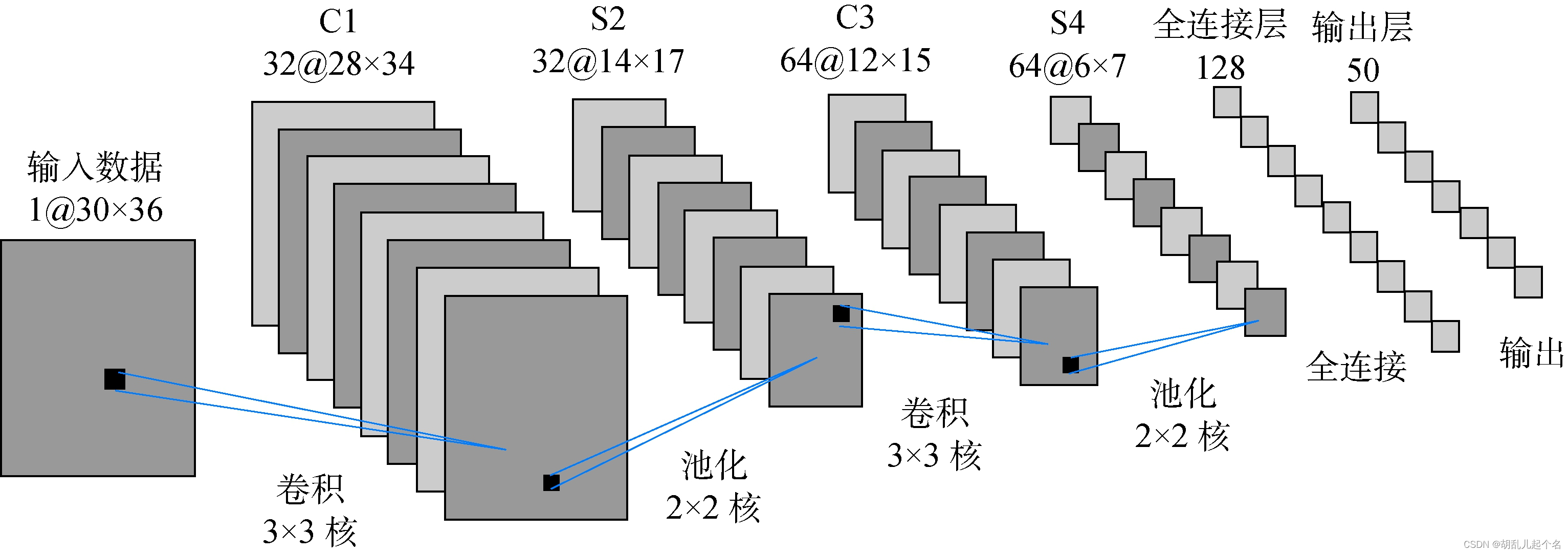
一、卷积神经网络示例

  卷积神经网络（CNN）的基本组成包括输入层、卷积层、非线性激活函数、池化层和全连接层等部分。如下图所示，

• 输入层：输入层负责接收原始的输入数据，例如图像、文本等。在图像处理中，输入层通常是将图像转换为像素矩阵的形式。
• 卷积层：卷积层是CNN的核心部分，通过卷积运算对输入数据进行特征提取。每个卷积层包含若干个卷积核，每个卷积核都独立地对输入数据进行卷积操作，提取局部特征。卷积核的参数是通过训练自动学习得到的。
• 池化层：池化层对卷积层的输出进行下采样，从而减少数据的维度和计算量，同时保留重要特征。池化操作可以是最大池化、平均池化等形式。
• 全连接层：全连接层通常位于CNN的末端，负责将前面层次提取到的特征进行整合和分类。全连接层的神经元与前一层的所有神经元都相连，根据前一层的输出计算输出值。
• 非线性激活函数：激活函数引入了非线性因素，使得CNN能够更好地学习和模拟复杂的特征。常用的激活函数有ReLU、Sigmoid和Tanh等。
    可以把它想象成为一个图片分类任务，比如你想对手写数字图片进行识别，那么这里的输入便会是一个图片，经过一系列的网络最后经过激活函数softmax层进行输出，softmax层会根据你的训练集的类别输出一个概率，比如这里我们需要识别0-9这10个数字，那么就会输出10个分别为每个类别的概率。

二、卷积层

1.卷积核

  在卷积神经网络（CNN）中，卷积核被用作过滤器，以提取图像的局部特征。

  如图所示，输入的是原始图像，每一个数字都代表像素，中间的是卷积核，图中显示的是卷积核的一次工作过程，通过卷积核的计算输出了一个结果，计算方式就是将对应位置的数据相乘然后相加，遵循的原则是卷积核从左往右移动，在从上往下移动。如下图所示：

  如果我们的原始输入数据都是图像，那么我们定义的卷积核窗口的宽度和高度要比输入图像的宽度和高度小，较常用的卷积核窗口的宽度和高度大小是3x3和5x5。在定义卷积核的深度时，只要保证与输入图像的色彩通道一致就可以了，如果输入图像是3个色彩通道的，那么卷积核的深度就是3:如果输入图像是单色彩通道的，那么卷积核的深度就是1，以此类推，如图所示为单色彩通道的输入图像的卷积过程。

2.padding

  下面，根据我们定义的卷积核步长对卷积核窗口进行滑动。卷积核的步长其实就是卷积核窗口每次滑动经过的图像上的像素点数量，如图所示是一个步长为2的卷积核经过一次滑动后窗口位置发生的变化。

  如果我们仔细观察,则还会发现在图中输入图像的最外层多了一圈全为0的像素这其实是一种用于提升卷积效果的边界像素填充方式。我们在对输入图像进行卷积之前，有两种边界像素填充方式可以选择，分别是Same和Valid。Valid方式就是直接对输入图像进行卷积，不对输入图像进行任何前期处理和像素填充，这种方式的缺点是可能会导致图像中的部分像素点不能被滑动窗口捕捉;Same方式是在输入图像的最外层加上指定层数的值全为0的像素边界，这样做是为了让输入图像的全部像素都能被滑动窗口捕捉。

• valid意味着不做卷积，所以如果你有一个nxn的图像和一个fxf的卷积核，那么你的输出就是(n-f+1)x(n-f+1)。
• 当使用same做填充时，你的输出就会是(n+2p-f+1)x(n+2p-f+1)。

3.步长（stride）

  步长（stride）在卷积神经网络中是指卷积核在图像上滑动的距离。在卷积操作中，步长决定了卷积核每次移动的像素数量。通过调整步长，可以在一定程度上控制特征提取的速度和精度。较小的步长会导致卷积核在图像上滑动较慢，提取的特征更加精细，但会增加计算的复杂度和时间成本。较大的步长则会使卷积核在图像上快速滑动，减少计算量和时间成本，但可能会降低特征提取的精度。

  通过对卷积过程的计算，我们可以总结出一个通用公式，在本书中我们统一把它叫作卷积通用公式，用于计算输入图像经过一轮卷积操作后的输出图像的宽度和高度的参数，公式如下:

  其中，通用公式中的即和H分别表示图像的宽度(Weight)和高度(Height)的值;下标 input 表示输入图像的相关参数;下标ouiput表示输出的图像的相关参数:下标filter表示卷积核的相关参数;S表示卷积核的步长:P(是Padding的缩写)表示在图像边缘增加的边界像素层数，如果图像边界像素填充方式选择的是Same模式，那么P的值就等于图像增加的边界层数，如果选择的是Valid模式，那么P=0。
  下面看一个具体的实例。输入一个7x7x1的图像数据，卷积核窗口为3x3x1，输入图像的最外层使用了一层边界像素填充，卷积核的步长stride为1，然后根据公式就能够计算出最后输出特征图的宽度和高度都是7.

4.三维卷积

  我们已经了解了单通道的卷积操作过程，但是在实际应用中一般很少处理色彩通道只有一个的输入图像，所以接下来看看如何对三个色彩通道的输入图像进行卷积操作，如图：

  在卷积过程中我们还加入了一个值为1的偏置，其实整个计算过程和之前的单通道的卷积过程大同小异，我们可以将三通道的卷积过程看作三个独立的单通道卷积过程，最后将三个独立的单通道卷积过程的结果进行相加，就得到了最后的输出结果。

卷积核的通道数等于输入图像的通道数
卷积核的个数等于输出通道

二、池化层

  卷积神经网络中的池化层可以被看作卷积神经网络中的一种提取输入数据的核心特征的方式，不仅实现了对原始数据的压缩，还大量减少了参与模型计算的参数，从某种意义上提升了计算效率。其中，最常被用到的池化层方法是平均池化层和最大池化层，池化层处理的输入数据在一般情况下是经过卷积操作之后生成的特征图。如图所示是一个最大池化层的操作过程,平均池化同理。

池化层不仅能够最大限度地提取输入的特征图的核心特征，还能够对输入的特征图进行压缩。

三、全连接层

  全连接层的主要作用是将输入图像在经过卷积和池化操作后提取的特征进行压缩，并且根据压缩的特征完成模型的分类功能。如图所示是一个全连接层的简化流程。

  其实全连接层的计算比卷积层和池化层更简单，如图所示的输入就是我们通过卷积层和池化层提取的输入图像的核心特征，与全连接层中定义的权重参数相乘，最后被压缩成仅有的10个输出参数，这10个输出参数其实已经是一个分类的结果，再经过激活函数的进一步处理，就能让我们的分类预测结果更明显。将10个参数输入到Softmax激活函数中，激活函数的输出结果就是模型预测的输入图像对应各个类别的可能性值。

四、AlexNet模型示例

  AlexNet模型是一个在深度学习领域具有重要影响的卷积神经网络（CNN）模型。它在2012年的ImageNet图像分类挑战赛中赢得了冠军，证明了CNN在复杂模型下的有效性。AlexNet模型使用GPU进行训练，使得在大数据上的训练在可接受的时间范围内得到结果。

• (1)INPUT层:为输入层，AlexNet卷积神经网络默认的输入数据必须是维度为224x224x3的图像，即输入图像的高度和宽度均为224，色彩通道是R、G、B三个。
• (2)Conv1层:为AlexNet的第1个卷积层，使用的卷积核滑动窗口为11x11x3，步长为4，Padding为2。通过套用卷积通用公式，可以得到最后输出的特征图的高度和宽度均为55，即55=(224-11+4)/4+1，同时这个卷积层要求最后输出深度为96的特征图，所以需要进行96次卷积，最后得到输出的特征图的维度为55x55x96。
• (3)MaxPool1层:为AlexNet的第1个最大池化层,最大池化层的滑动窗口为3x3x96,步长为2。通过套用池化通用公式，可以得到最后输出的特征图的高度和宽度均为27，即27=(55-3)/2+1，最后得到的输出的特征图的维度为27x27x96。
• (4)Conv2层:为AlexNet的第2个卷积层，使用的卷积核滑动窗口为5x5x96，步长为1，Padding为2。通过套用卷积通用公式，可以得到最后输出的特征图的高度和宽度均为27，即27=27-5+4+1，同时这个卷积层要求最后输出深度为256的特征图，所以需要进行256次卷积，最后得到输出的特征图的维度为27x27x256。
• (5)**MaxPool2层:**为AlexNet的第2个最大池化层。最大池化层的滑动窗口为3x3x256,步长为2。通过套用池化通用公式，可以得到最后输出的特征图的高度和宽度均为13，即13=(27-3)/2+1，最后得到输出的特征图的维度为13x13x256。
• (6)Conv3层:为AlexNet的第3个卷积层，使用的卷积核维度为3x3x256，步长为1，Padding为1。通过套用卷积通用公式，可以得到最后输出的特征图的高度和宽度均为13-3+2+1，同时这个卷积层要求最后输出深度为384的特征图，所以需要进行384次卷积，最后得到特征图的维13x13x384。
• (7)Conv4层:为AlexNet的第4个卷积层，使用的卷积核滑动窗口为3x3x384，步长为1，Padding为1。通过套用卷积通用公式，可以得到最后输出的特征图的高度和宽度均为13，即13=13-3+2+1，同时这个卷积层要求最后输出深度依旧为384的特征图，所以需要进行384次卷积，最后得到输出的特征图的维度为13x13x384。
• (8)Conv5层:为AlexNet的第5个卷积层，使用的卷积核滑动窗口为3x3x384，步长为1，Padding为1。通过套用卷积通用公式，可以得到最后输出的特征图的高度和宽度13-3+2+1，同时这个卷积层要求最后输出深度为256的特征图，所以需要进行256次卷积，最后得到输出的特征图的维度为13x13x256。
• (9)MaxPool3层:为AlexNet的第3个最大池化层，最大池化层的滑动窗口为3x3x256，步长为2。通过套用池化通用公式，可以得到最后输出的特征图的高度和宽度均6=(13-3)/2+1，最后得到输出的特征图的维度为 6x6x256。
• (10)FC6层:为AlexNet的第1个全连接层，输入的特征图的维度为6x6x256，首先要对输入的特征图进行扁平化处理，将其变成维度为1x9216的输入特征图，因为本层要求输出数据的维度是1x4096，所以需要一个维度为9216x4096的矩阵完成输入数据和输出数据的全连接，最后得到输出数据的维度为1x4096。
• (11)FC7层:为AlexNet的第2个全连接层，输入数据的维度为1x4096，输出数据的维度仍然1x4096，所以需要一个维度为4096x4096的矩阵完成输入数据和输出数据的全连接，最后得到输出数据的维度依旧为1x4096。
• (12)FC8层:为AlexNet的第3个全连接层，输入数据的维度为1x4096，输出数据的维度要求是1x1000，所以需要一个维度为4096x1000的矩阵完成输入数据和输出数据的全连接，最后得到输出数据的维度为1x1000。
• (13)OUTPUT层:为输出层，要求最后得到输入图像对应1000个类别的可能性值，因为AlexNet用来解决图像分类问题，即要求通过输入图像判断该图像所属的类别，所以我们要将全连接层最后输出的维度为1x1000的数据传递到Softmax激活函数中，就能得到1000个全新的输出值，这1000个输出值就是模型预测的输入图像对应1000个类别的可能性值。

五、AlexNet代码示例

import os
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import layers,losses, metrics
from data_process.data_manager import get_dataset
from network.alexnet import AlexNet

class TrainModel():
    def __init__(self, lr=0.01):
        self.model = AlexNet(num_classes=2)                # 定义网络,2分类
        self.model.build(input_shape=(None, 112, 112, 3))  # BHWC
        self.model.summary()
        self.loss_fun = losses.CategoricalCrossentropy()    # 定义损失函数, 这里交叉熵
        self.opt = tf.optimizers.SGD(learning_rate=lr)      # 随机梯度下降优化器
        self.train_acc_metric = metrics.CategoricalAccuracy()   # 设定统计参数
        self.val_acc_metric = metrics.CategoricalAccuracy()

    def train(self, fpath="./data/mycatdog2", epochs=300, m=5):
        """ 训练网络 """
        batch_size = 64
        test_acc_list = []
        # 读取数据集
        train_dataset = get_dataset(os.path.join(fpath, "train"), is_shuffle=True, batch_size=batch_size)
        val_dataset = get_dataset(os.path.join(fpath, "valid"), is_shuffle=False, batch_size=batch_size)
        # 训练
        loss_val = 0
        for epoch in range(epochs):
            print(" ** Start of epoch {} **".format(epoch))
            # 每次获取一个batch的数据来训练
            for nbatch, (inputs, labels) in enumerate(train_dataset):
                with tf.GradientTape() as tape:                 # 开启自动求导
                    y_pred = self.model(inputs, training=True)  # 前向计算  
                    loss_val = self.loss_fun(labels, y_pred)    # 误差计算
                    grads = tape.gradient(loss_val, self.model.trainable_variables)         # 梯度计算
                    self.opt.apply_gradients(zip(grads, self.model.trainable_variables))    # 权重更新
                    self.train_acc_metric(labels, y_pred)   # 更新统计传输
                    if nbatch % m == 0: # 打印
                        correct = tf.equal(tf.argmax(labels, 1), tf.argmax(y_pred, 1))
                        acc = tf.reduce_mean(tf.cast(correct, tf.float32))
                        print('{}-{} train_loss:{:.5f}, train_acc:{:.5f}'.format(epoch, nbatch, float(loss_val), acc))
            # 输出统计参数的值
            train_acc = self.train_acc_metric.result()
            self.train_acc_metric.reset_states()
            print('Training acc over epoch: {}, acc:{:.5f}'.format(epoch, float(train_acc)))
            # 每次迭代在验证集上测试一次
            for nbatch, (inputs, labels) in enumerate(val_dataset):
                y_pred = self.model(inputs)
                self.val_acc_metric(labels, y_pred)
            val_acc = self.val_acc_metric.result()
            self.val_acc_metric.reset_states()
            print('Valid acc over epoch: {}, acc:{:.5f}'.format(epoch, float(val_acc)))
            test_acc_list.append(val_acc)
        # 训练完成保存模型
        tf.saved_model.save(self.model, "./output/mnist_model")
        # 画泛化能力曲线(横坐标是epoch, 测试集上的精度),并保存
        x = np.arange(1, len(test_acc_list)+1, 1)
        y = np.array(test_acc_list)
        plt.plot(x, y)
        plt.xlabel("epoch")
        plt.ylabel("val_acc")
        plt.title('model acc in valid dataset')
        plt.savefig("./output/val_acc.png", format='png')

if __name__ == "__main__":
    path = "./output"
    if not os.path.exists(path):
        os.makedirs(path)
    model = TrainModel()
    model.train(fpath="F:\数据集\mycatdog2")