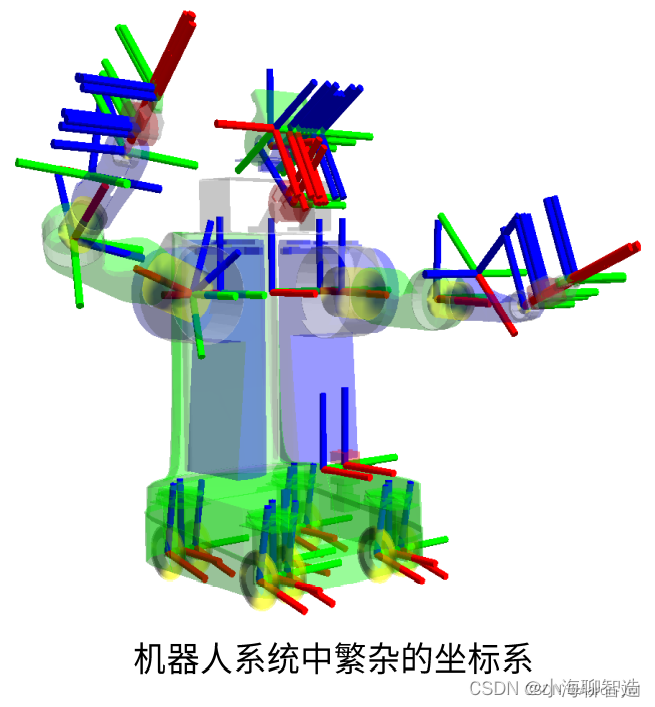
坐标系是我们非常熟悉的一个概念，也是机器人学中的重要基础，在一个完整的机器人系统中，会存在很多坐标系，这些坐标系之间的位置关系该如何管理？
ROS给我们提供了一个坐标系的管理神器——TF。

比如在机械臂形态的机器人中，机器人安装的位置叫做基坐标系Base Frame，机器人安装位置在外部环境下的参考系叫做世界坐标系World Frame，机器人末端夹爪的位置叫做工具坐标系，外部被操作物体的位置叫做工件坐标系，在机械臂抓取外部物体的过程中，这些坐标系之间的关系也在跟随变化。

一、机器人中的坐标变换

机器人运动学的核心，描述任意两个坐标系之中任意两个向量之间的变换，可以用一个4×4的变换矩阵（Transformation Matrices）来描述它的平移和旋转变化。
变换矩阵中有包括旋转矩阵（Rotation Matrix）的信息和位置移动（Translation）的信息

二、TF功能包

一个机器人系统中，通常会涉及到很多坐标系的运算，这免不了大量的矩阵运算。我们可以使用ROS中的TF(Transform)功能包来解决问题。

TF功能包的特点：默认能记录10秒内机器人所有坐标系的位置关系。

TF坐标变化如何实现？

• 广播TF变换
• 监听TF变换

在ROS Master启动后，启动TF后，会在后台维护一个名为“TF树（TF Tree）”的数据结构。所有的坐标系都是通过树形结构保存在这个树结构当中，当有结点想查询某两个坐标系之间的关系的话，直接可以查询这个TF Tree来得到。

比如这个TF的例子：

这辆带激光雷达的车，车体是以base_link为坐标系的，激光雷达是以base_laser为坐标系的，可以看到base_laser是base_link向x轴平移了0.1m，向z轴平移了0.2m，y轴没有平移。

当base_laser测到离墙面的距离为0.3m，即向量(0.3,0,0)时，就可以根据图下方的TF tree进行坐标系之间的数据变换的运算，从而算出base_link的相对与测距点的相对向量(0.4,0,0.2)。

也就是你不用计算两个东西的位置检测，算其中的一个，然后根据他们相对的差距来计算另一个零件的坐标位置

三、小海龟跟随实验

我们通过一个小程序来实现小海龟跟随另一个小海龟的实验，并通过可视化的方法来理解坐标系的变换

在这个实验中，我们先生成一只小乌龟，然后再生成一只新的小乌龟，新的小乌龟会自动跟随旧的小乌龟，直到重合。

3.1 启动实验
在进行实验之前，由于noetic的版本是预制了这个程序的，但是直接运行会报错，原因是python解释器的指向问题，我们先打开终端输入以下命令：

cd /usr/bin/
sudo rm -r python #出现rm -r 找不到文件的忽略即可
sudo cp python3 python

执行完后我们就可以运行这个程序了：

roslaunch turtle_tf turtle_tf_demo.launch

启动键盘控制

 rosrun turtlesim turtle_teleop_key

打开后我们就会生成两只小乌龟，我们通过键盘控制其中一只小乌龟，另一只就会自动跟随。

3.2 查看当前的TF树

我们可以查看当前的TF数，查看坐标系之间的关系：

rosrun tf view_frames

但是直接运行会报错，无法生成pdf文件

我们打开如图所示的报错文件夹，加上如图所示的这句话：

再运行：

rosrun tf view_frames

成功生成了pdf文件：

我们可以看到这棵树展示了当前坐标系之间的位置关系，turtle1和turtle2是相对于world坐标系变化的。

3.3 坐标相对位置可视化
3.3.1 tf_echo
我们如果想看两只小海龟的相对变换关系，可输入：

rosrun tf tf_echo turtle1 turtle2

我们如果操控小海龟移动，则位置会发生变化：

3.3.2 rviz
我们可以打开rviz工具：

rosrun rviz rviz -d `rospack find turtle_tf` /rviz/turtle_rviz.rviz

打开界面之后，在上面的Fixed Frame选择world
在左下角的add添加TF。就可以看到三个坐标系了。

最后，控制小海龟运动，坐标系发生改变，然后坐标系turtle2原点会靠近turtle1原点

下图中左边变换矩阵的运算，其实就是坐标移动的本质。两个坐标系相对于world坐标系的变换的乘积可以求得两个坐标系相对的变换关系。

rviz的中心点位置对应小乌龟的左下 0.0 点

有一个简单的认知概念吧，上面大部分的来自于这个文章，文中有个控制小乌龟的怎么控制走动起来的没说明，我做下补充，
https://blog.csdn.net/weixin_56197703/article/details/127098905